已知x、y、z是三个非负整数,满足3x+2y+z=5,x+y-z=2,若s=2x+y-z,则s的最大值与最小值的和为 .
【答案】
分析:根据题意,先推断出S取最大值与最小值时的x、y、z的值,再求S的最大值与最小值的和.
解答:解:法1:要使S取最大值,2x+y最大,z最小,
∵x、y、z是三个非负整数,
∴z=0,解方程组
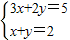
,解得:
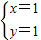
,
∴S的最大值=2×1+1-0=3;
要使S取最小值,
联立得方程组
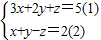
,
(1)+(2)得4x+3y=7,y=
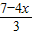
,
(1)-(2)×2得,x+3z=1,z=
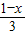
,
把y=
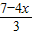
,z=
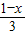
代入S=2x+y-z,整理得,S=x+2,当x取最小值时,S有最小值,
∵x、y、z是三个非负整数,
∴x的最小值是0,
∴S
最小=2,
∴S的最大值与最小值的和:3+2=5;
法2:∵x+y-z=2,S=2x+y-z,
∴S=x+2,
∵3x+2y+z=5,x+y-z=2,
∴y=
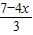
或z=
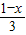
,
∵x,y,z为三个非负有理数,
∴
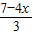
≥0①,

≥0②,
解不等式①得,x≤

,
解不等式②得,x≤1,
∴x≤1,
又x,y,z为三个非负有理数,
∴0≤x≤1,
∴S的最大值3,最小值2,
则S的最大值与最小值的和:3+2=5.
故答案为:5.
点评:本题考查了函数的最值问题.解答时,在给定的范围内(x、y、z是三个非负整数),求一个代数式s=2x+y-z的最值问题,难度较大.所以采取了化归思想,例如,将问题转化为“要使S取最大值,2x+y最大,z最小”.

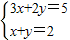 ,解得:
,解得: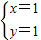 ,
,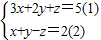 ,
,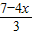 ,
,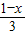 ,
,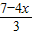 ,z=
,z=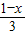 代入S=2x+y-z,整理得,S=x+2,当x取最小值时,S有最小值,
代入S=2x+y-z,整理得,S=x+2,当x取最小值时,S有最小值,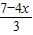 或z=
或z=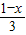 ,
,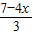 ≥0①,
≥0①, ≥0②,
≥0②, ,
,