
| 进价(元/盏) | 售价(元/盏) | |
| A | 30 | 45 |
| B | 50 | 70 |
分析 (1)设购进A型台灯x盏,销售完这100盏台灯共获利润y元,则购进B型台灯(100-x)盏,根据总利润=每台A型台灯利润×购进数量+每台B型台灯利润×购进数量,即可找出y与x的函数表达式;
(2)由总价=每台A型台灯单价×购进数量+每台B型台灯单价×购进数量,即可得出关于x的一元一次方程,解之即可得出x的值,将其代入(1)的结论中求出y值即可.
解答 解:(1)设购进A型台灯x盏,销售完这100盏台灯共获利润y元,则购进B型台灯(100-x)盏,
根据题意得:y=(45-30)x+(70-50)(100-x)=-5x+2000.
(2)根据题意得:30x+50(100-x)=3500,
解得:x=75,
∴y=-5x+2000=1625.
答:若商场预计进货款为3500元,则销售完这两种台灯的利润为1625元.
点评 本题考查了一次函数的应用以及一元一次方程的应用,解题的关键是:(1)根据总利润=每台A型台灯利润×购进数量+每台B型台灯利润×购进数量,找出y与x的函数表达式;(2)根据总价=每台A型台灯单价×购进数量+每台B型台灯单价×购进数量,列出关于x的一元一次方程.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $3\sqrt{15}÷\sqrt{3}=3\sqrt{5}$ | B. | a2×a3=a6 | C. | a2+a=a3 | D. | (-2a2)3=-6a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
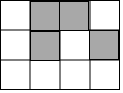 如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
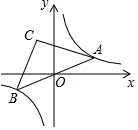 如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.
如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
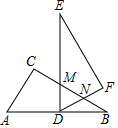 如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com