
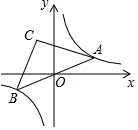
 如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.
如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$. 分析 连结OC,作CD⊥x轴于D,AE⊥x轴于E,利用反比例函数的性质和等腰直角三角形的性质,根据“AAS”可判定△COD≌△OAE,设A点坐标为(a,$\frac{6}{a}$),得出OD=AE=$\frac{6}{a}$,CD=OE=a,最后根据反比例函数图象上点C的坐标特征确定函数解析式.
解答 解:如图,连结OC,作CD⊥x轴于D,AE⊥x轴于E,
∵A点、B点是正比例函数图象与双曲线y=$\frac{6}{x}$的交点,
∴点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等腰直角三角形,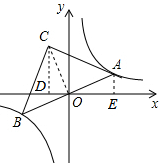
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
∵在△COD和△OAE中,
$\left\{\begin{array}{l}{∠DCO=∠AOE}\\{∠ODC=∠AEO}\\{OC=OA}\end{array}\right.$,
∴△COD≌△OAE(AAS),
设A点坐标为(a,$\frac{6}{a}$),则OD=AE=$\frac{6}{a}$,CD=OE=a,
∴C点坐标为(-$\frac{6}{a}$,a),
∵-$\frac{6}{a}$•a=-8,
∴点C在反比例函数y=-$\frac{6}{x}$图象上.
故答案为:y=-$\frac{6}{x}$.
点评 本题主要考查了用待定系数法求反比例函数的解析式,解题时需要综合运用反比例函数图象上点的坐标特征、等腰直角三角形的性质.判定三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.
如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
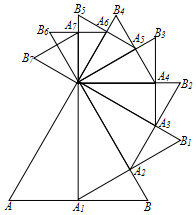 已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a..
已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
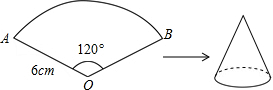 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )| A. | 4πcm2 | B. | 6πcm2 | C. | 9πcm2 | D. | 12πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/盏) | 售价(元/盏) | |
| A | 30 | 45 |
| B | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
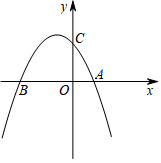 如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.
如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com