
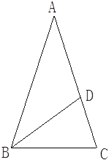
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,
(1)求证:△ABC∽△BCD;
(2)若BC=2,求AB的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)根据角平分线的性质得到∠DBC=∠A,已知有一组公共角,则根据有两组角对应相等则两三角形相似可得到△ABC∽△BCD;
(2)相似三角形的对应边对应成比例,且由已知可得到BD=BC=AD,从而便可求得AB的长.
试题解析:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°.
∴∠DBC=∠A=36°.
又∵∠ABC=∠C,
∴△ABC∽△BCD.
(2)∵∠ABD=∠A=36°,
∴AD=BD,∠BDC=∠C=72°.
∴BD=BC=AD.
∵△ABC∽△BCD,
∴![]() .
.
即![]() .
.
解得:AB=![]() 或
或![]() (不符合题意).
(不符合题意).
∴AB=![]() .
.
考点: 1.等腰三角形的性质;2.角平分线的性质;3.相似三角形的判定与性质.


科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是菱形,边BC在x轴上,点A(0,4),点B(3,0),双曲线y=![]() 与直线BD交于点D、点E.
与直线BD交于点D、点E.
(1)求k的值;
(2)求直线BD的解析式;
(3)求△CDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
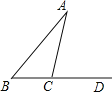
【题目】如图所示,在![]() 中,
中,![]() 是钝角,让点C在射线BD上向右移动,则( )
是钝角,让点C在射线BD上向右移动,则( )
A.![]() 将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
B.![]() 将变成锐角三角形,而不会再是钝角三角形
将变成锐角三角形,而不会再是钝角三角形
C.![]() 将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.![]() 先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,角形然后再次变为钝角三角形
先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,角形然后再次变为钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
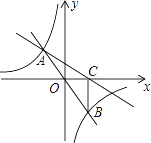
【题目】如图,直线y=mx(m为常数,且m≠0)与双曲线y= ![]() (k为常数,且k≠0)相交于A(﹣2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为________.
(k为常数,且k≠0)相交于A(﹣2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
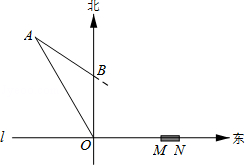
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
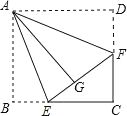
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com