
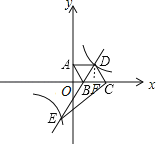
【题目】如图所示,四边形ABCD是菱形,边BC在x轴上,点A(0,4),点B(3,0),双曲线y=![]() 与直线BD交于点D、点E.
与直线BD交于点D、点E.
(1)求k的值;
(2)求直线BD的解析式;
(3)求△CDE的面积.

【答案】(1)20;(2)y=2x﹣6;(3)35.
【解析】
(1)先求出D点的坐标,再代入求出即可;
(2)设直线BD的解析式为y=ax+b,把B(3,0),D(5,4)代入得出方程组,求出方程组的解即可;
(3)求出E点的坐标,分别求出△CBD和△CBE的面积,即可得出答案.
(1)∵点A(0,4),点B(3,0),
∴OA=4,OB=3,
由勾股定理得:AB=5,
过D作DF⊥x轴于F,则∠AOB=∠DFC=90°,
∵四边形ABCD是菱形,
∴AB=DC=CD=AD=5,AD∥BC,
∴AO=DF=4,
∵AD∥BC,AO⊥OB,DF⊥x轴,
∴∠DAO=∠AOF=∠DFO=90°,
∴四边形AOFD是矩形,
∴AD=OF=5,
∴D点的坐标为(5,4),
代入y=![]() 得:k=5×4=20;
得:k=5×4=20;
(2)设直线BD的解析式为y=ax+b,
把B(3,0),D(5,4)代入得:![]() ,
,
解得:a=2,b=﹣6,
所以直线BD的解析式是y=2x﹣6;
(3)由(1)知:k=20,
所以y=![]() ,
,
解方程组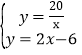 得:
得:![]() ,
,![]() ,
,
∵D点的坐标为(5,4),
∴E点的坐标为(2,10),
∵BC=5,
∴△CDE的面积S=S△CDB+S△CBE=![]() +
+![]() =35.
=35.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
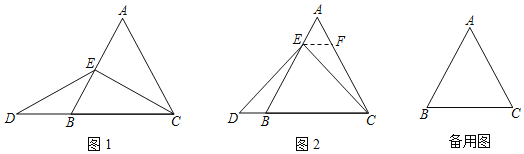
(2)特例启发,解决问题:解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题:在等边三角形ABC中,点E在AB的延长线上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=3,求CD的长.(请画出符合题意的图形,并直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师买了一套带有屋顶花园的住房,为了美化居住环境,张老师准备用100元钱买4株月季花,2株黄果兰种在花园中.已知3株月季花、4株黄果兰共需158元,2株月季花、3株黄果兰共需117元.问:张老师用100元钱能否买回他所需要的花卉?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方体纸盒的表面积为12cm2;

(1)求正方体的棱长;
(2)剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?
(3)一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
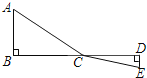
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
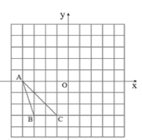
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出△ABC关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标;
(2)连接BC′,B′C,求四边形BCB′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com