Question

【题目】数学课上，李老师出示了如下框中的题目．

小敏与同桌小聪讨论后，进行了如下解答：

（1）特殊情况，探索结论:当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：AE　 　DB（填“＞”，“＜”或“＝”）．

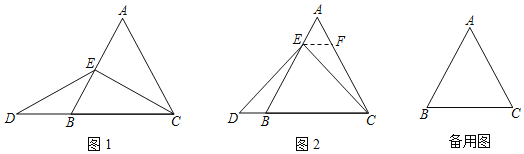
（2）特例启发，解决问题:解：题目中，AE与DB的大小关系是：AE　 　DB（填“＞”，“＜”或“＝”）．理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）

（3）拓展结论，设计新题:在等边三角形ABC中，点E在AB的延长线上，点D在直线BC上，且ED＝EC．若△ABC的边长为2，AE＝3，求CD的长．（请画出符合题意的图形，并直接写出结果）

Answer 1

【答案】（1）＝；（2）＝，理由见解析；（3）5

【解析】

（1）先证明BD=BE即可解决问题；
（2）作EF∥BC交AC于F．证得△DBE≌△EFC，得出BD=EF=AE，所以BD=AE；
（3）作EF∥BC交AC的延长线于F，证出△EBD≌△CFE，可得BD=EF=AE=3，CD=BD+BC=3+2=5．

解：（1）如图1中，

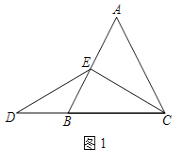
∵△ABC是等边三角形，AE＝EB，

∴∠BCE＝∠ACE＝30°，∠ABC＝60°，

∵ED＝EC，

∴∠D＝∠ECD＝30°，

∵∠EBC＝∠D+∠BED，

∴∠D＝∠BED＝30°，

∴BD＝BE＝AE．

故答案为：＝；

（2）结论：AE＝BD．理由如下：

如图2中，作EF∥BC交AC于F．

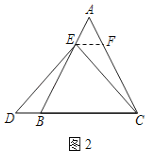
∵∠AEF＝∠B＝60°，∠A＝60°，

∴△AEF是等边三角形，

∴AE＝EF＝AF，∠AFE＝60°，

∴∠EFC＝∠DBE＝120°，

∵AB＝AC，AE＝AF，

∴BE＝CF，

∵∠D＝∠ECB＝∠CEF，且∠DBE＝∠EFC，BE＝CF，

∴△DBE≌△EFC（AAS），

∴BD＝EF＝AE，

∴BD＝AE，

故答案为：＝；

（3）如图3中，当E在AB的延长线上时，作EF∥BC交AC的延长线于F，

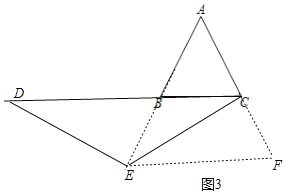
∵EF∥BC，

∴∠BCE＝∠CEF，∠ABC＝∠AEF＝60°，∠ACB＝∠AFE＝60°，

∴△AEF是等边三角形，

∴AE＝EF＝AF＝3，

∴BE＝CF，

∵DE＝CE，

∴∠EDC＝∠DCE，

∴∠EDC＝∠CEF，且BE＝CF，∠F＝∠ABC＝∠DBE＝60°，

∴△DBE≌△EFC（AAS）

∴BD＝EF＝3，

∴CD＝DB+BC＝3+2＝5．