
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

【答案】(1)图见解析;(2)126°;(3)525.
【解析】
(1)利用被调查学生的人数=了解程度达到B等的学生数÷所占比例,即可得出被调查学生的人数,由了解程度达到C等占到的比例可求出了解程度达到C等的学生数,再利用了解程度达到A等的学生数=被调查学生的人数-了解程度达到B等的学生数-了解程度达到C等的学生数-了解程度达到D等的学生数可求出了解程度达到A等的学生数,依此数据即可将条形统计图补充完整;
(2)根据A等对应的扇形圆心角的度数=了解程度达到A等的学生数÷被调查学生的人数×360°,即可求出结论;
(3)利用该校现有学生数×了解程度达到A等的学生所占比例,即可得出结论.
(1)48÷40%=120(人),
120×15%=18(人),
120-48-18-12=42(人).
将条形统计图补充完整,如图所示.

(2)42÷120×100%×360°=126°.
答:扇形统计图中的A等对应的扇形圆心角为126°.
(3)1500×![]() =525(人).
=525(人).
答:该校学生对政策内容了解程度达到A等的学生有525人.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
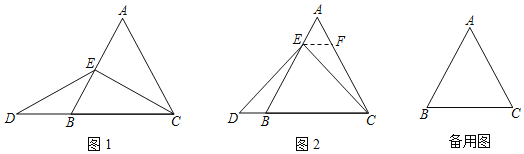
(2)特例启发,解决问题:解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题:在等边三角形ABC中,点E在AB的延长线上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=3,求CD的长.(请画出符合题意的图形,并直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;

(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=20°,M,N分別是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A.β﹣α=30°B.β﹣α=40°C.β+α=180°D.β+α=200°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师买了一套带有屋顶花园的住房,为了美化居住环境,张老师准备用100元钱买4株月季花,2株黄果兰种在花园中.已知3株月季花、4株黄果兰共需158元,2株月季花、3株黄果兰共需117元.问:张老师用100元钱能否买回他所需要的花卉?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
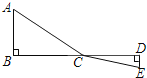
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com