
【题目】小强家有一块三角形菜地,量得两边长分别为![]() ,
,![]() ,第三边上的高为
,第三边上的高为![]() .请你帮小强计算这块菜地的面积.(结果保留根号)
.请你帮小强计算这块菜地的面积.(结果保留根号)
【答案】(600±150![]() )
)![]()
【解析】
试题本题需要分两种情况求出第三边的长度,然后计算面积.
试题解析:分两种情况:
(1)如图(1)
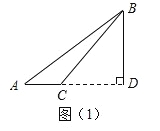
当∠ACB为钝角时,∵BD是高, ∴∠D=90°.
在Rt△BCD中,BC=40,BD=30 ∴CD=![]()
在Rt△ABD中,AB=50, ∴AD=![]() =40
=40
∴AC=AD-CD=40-10![]() ∴S=(40-10
∴S=(40-10![]() )×30÷2=(600-150
)×30÷2=(600-150![]() )
)![]()
(2)如图(2)
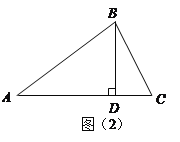
当∠ACB为锐角时,∵BD是高, ∴∠ADB=∠BDC=90°,
在Rt△BCD中,BC=40,BD=30 ∴CD=![]()
在Rt△ABD中,AB=50, ∴AD=![]() =40
=40
∴AC=AD+CD=40+10![]() ∴S=(40+10
∴S=(40+10![]() )×30÷2=(600+150
)×30÷2=(600+150![]() )
)![]()
综上所述:S= (600±150![]() )
)![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 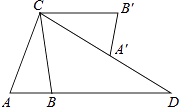
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
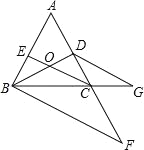
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E,F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.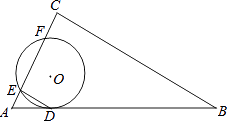
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
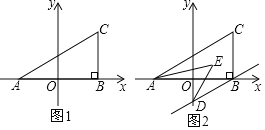
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过点C作CB⊥x轴于点B.
=0,过点C作CB⊥x轴于点B.
(1)求A、C两点坐标;
(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
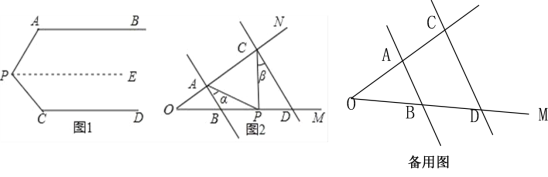
【题目】问题情境:如图1,AB∥CD,∠PAB=125°,∠PCD=135°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度。
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,①如果点P运动到D点右侧(不包括D点),则∠APC与α、β之间的数量关系为 .②如果点P运动到B点左侧(不包括B点),则∠APC与α、β之间的数量关系 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
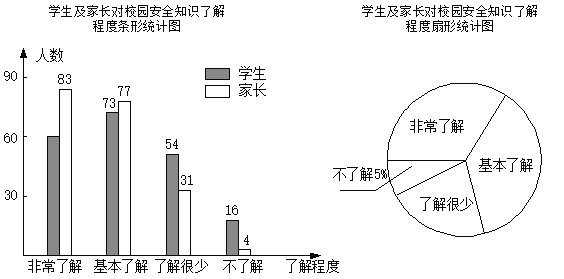
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.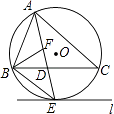
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com