
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.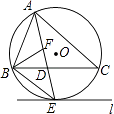
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
【答案】
(1)解:直线l与⊙O相切.
理由:如图1所示:连接OE、OB、OC.
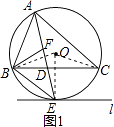
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴ ![]() .
.
∴∠BOE=∠COE.
又∵OB=OC,
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)解:∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)解:由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴ ![]() ,即
,即 ![]() ,解得;AE=
,解得;AE= ![]() .
.
∴AF=AE﹣EF= ![]() ﹣7=
﹣7= ![]()
【解析】(1)由AE平分∠BAC,得到∠BAE=∠CAE,弧BE=弧CE,得到∠BOE=∠COE,又OB=OC,得到OE⊥BC因为l∥BC,得到OE⊥l,所以直线l与⊙O相切;(2)由BF平分∠ABC,得到∠ABF=∠CBF,又∠CBE=∠CAE=∠BAE,得到∠CBE+∠CBF=∠BAE+∠ABF,又∠EFB=∠BAE+∠ABF,得到∠EBF=∠EFB.所以BE=EF;(3)由(2)得BE=EF=DE+DF=7,因为∠DBE=∠BAE,∠DEB=∠BEA,得到△BED∽△AEB,得出比例,求得AE=![]() ,所以AF=AE﹣EF=
,所以AF=AE﹣EF=![]() ﹣7=
﹣7=![]() .
.


科目:初中数学 来源: 题型:
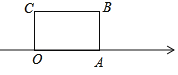
【题目】如图,面积为30的长方形OABC的边OA在数轴上,O为原点,OC=5.将长方形OABC沿数轴水平移动,O,A,B,C移动后的对应点分别记为O1, A1, B1, C1,移动后的长方形O1A1B1C1与原长方形OABC重叠部分的面积记为S
(1)当S恰好等于原长方形面积的一半时,数轴上点A1表示的数是多少?
(2)设点A的移动距离AA1=x
①当S=10时,求x的值;
②D为线段AA1的中点,点E在线段OO1上,且OE=![]() OO1,当点D,E所表示的数互为相反数时,求x的值.
OO1,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x(﹣x)2(﹣x)3;(2)x3x5﹣(2x4)2+x10÷x2.
(3)(﹣0.125)2018×82019;(4)(a﹣b)10÷(b﹣a)3÷(b﹣a)3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 ![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M. 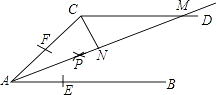
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题。
端午节期间,某食堂根据职工食用习惯,用700元购进甲、乙两种粽子260个,其中甲种粽子比乙种粽子少用100元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com