
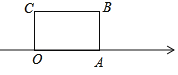
【题目】如图,面积为30的长方形OABC的边OA在数轴上,O为原点,OC=5.将长方形OABC沿数轴水平移动,O,A,B,C移动后的对应点分别记为O1, A1, B1, C1,移动后的长方形O1A1B1C1与原长方形OABC重叠部分的面积记为S
(1)当S恰好等于原长方形面积的一半时,数轴上点A1表示的数是多少?
(2)设点A的移动距离AA1=x
①当S=10时,求x的值;
②D为线段AA1的中点,点E在线段OO1上,且OE=![]() OO1,当点D,E所表示的数互为相反数时,求x的值.
OO1,当点D,E所表示的数互为相反数时,求x的值.
【答案】(1)A1表示的数是3或9;(2)①x=4,②x=![]() .
.
【解析】
(1)根据长方形的面积可得OA长即点A表示的数,在由已知条件得S=15,根据题意分情况讨论:①当向左移动时,②当向右移动时,根据长方形面积公式分别计算、分析即可得出答案.
(2)①由(1)知:OA=O1A1=6,OC=O1C1=5,由AA1=x得OA1=6-x,由长方形面积公式列出方程,解之即可.
②当向左移动时,由AA1=x得OA1=6-x,OO1=x,根据题意分别得出点E、点D表示的数,由点E和点D表示的数互为相反数列出方程,解之即可;当向右移动时,点D、E表示的数都是正数,不符合题意.
(1)解: ∵S长方形OABC=OA·OC=30,OC=5,
∴OA=6,
∴点A表示的数是6,
∵S=![]() S长方形OABC=
S长方形OABC=![]() ×30=15,
×30=15,
当向左移动时,
OA1·OC=15,
∴OA1=3,
∴A1表示的数是3;
②当向右移动时,
∴O1A·AB=15,
∴O1A=3,
∵OA=O1A1=6,
∴OA1=6+6-3=9,
∴A1表示的数是9;
综上所述:A1表示的数是3或9.
(2)解: ①由(1)知:OA=O1A1=6,OC=O1C1=5,
∵AA1=x,
∴OA1=6-x,
∴S=5×(6-x)=10,
解得:x=4.
②当长方形OABC沿数轴正方向运动时,点D,E表示的数均为正数,不符合题意;
当点D,E所表示的数互为相反数时,长方形OABC沿数轴负方向运动,画图如下: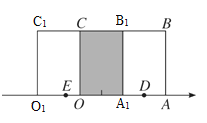
∵AA1=x,
∴OA1=6-x,OO1=x,
∴OE=![]() OO1=
OO1=![]() x,
x,
∴点E表示的数为-![]() x,
x,
又∵点D为AA1中点,
∴A1D=![]() AA1=
AA1=![]() x,
x,
∴OD=OA1+A1D=6-x+![]() x=6-
x=6-![]() x,
x,
∴点D表示的数为6-![]() x,
x,
又∵点E和点D表示的数互为相反数,
∴6-![]() x-
x-![]() x=0,
x=0,
解得:x=![]() .
.
故答案为:(1)A1表示的数是3或9;(2)①x=4,②x=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
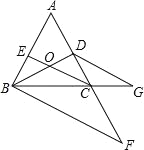
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
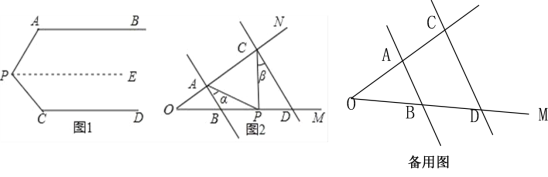
【题目】问题情境:如图1,AB∥CD,∠PAB=125°,∠PCD=135°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度。
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,①如果点P运动到D点右侧(不包括D点),则∠APC与α、β之间的数量关系为 .②如果点P运动到B点左侧(不包括B点),则∠APC与α、β之间的数量关系 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
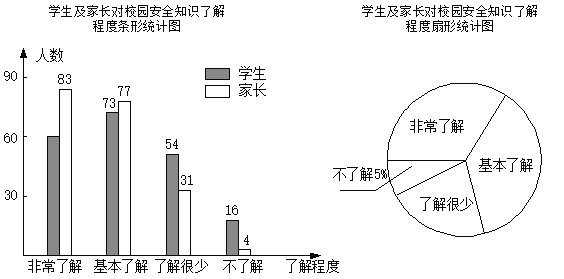
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
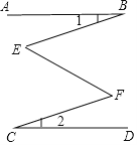
【答案】相等,理由见解析.
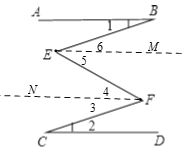
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.
【题型】解答题
【结束】
26
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣3),C(﹣4,﹣1).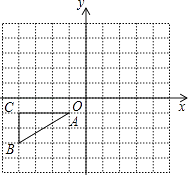
①作出△ABC关于原点O中心对称的图形;
②将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 , 画出△A1B1C1 , 并写出点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
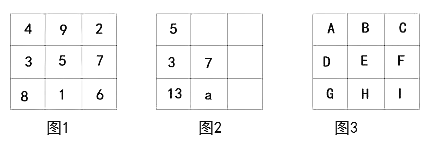
【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。
(1)如图2所示,求![]() 的值;
的值;
(2)如图3所示:
①若![]() 求整式D;
求整式D;
②若![]() 求这九个整式的和是多少。
求这九个整式的和是多少。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.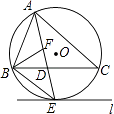
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com