练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算:

    （1）x（﹣x）2（﹣x）3；（2）x3x5﹣（2x4）2+x10÷x2．

    （3）（﹣0.125）2018×82019；（4）（a﹣b）10÷（b﹣a）3÷（b﹣a）3．

    【答案】（1）-；（2）-2；（3）8；（4）（b-a）4.

    【解析】

    本题需先根据整式的混和运算顺序和法则以及乘法公式分别进行计算，再把所得结果合并即可．

    解：（1）x（﹣x）2（﹣x）3

    = - xx2 x3

    =- x6；

    （2）x3x5﹣（2x4）2+x10÷x2

    =x8-4 x8+ x8

    =-2 x8；

    (3)原式=[（﹣0.125）×8]2018×8

    =1×8

    =8；

    （4））（a-b）10÷（b-a）3÷（b-a）3

    =（b-a）10÷（b-a）3÷（b-a）3

    ==（b-a）10-3-3
    =（b-a）4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于E，F两点，连结DE，已知∠B=30°，⊙O的半径为6，弧DE的长度为2π．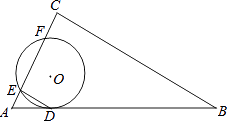

    （1）求证：DE∥BC；
    （2）若AF=CE，求线段BC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知,如图, AB∥CD，∠1=∠2，那么∠E和∠F相等吗? 为什么?

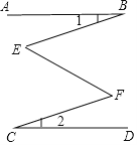
    【答案】相等，理由见解析.

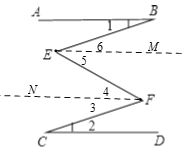
    【解析】试题分析：分别过E、F 点作CD的平行线EM、FN，根据平行线的性质得CD∥FN∥EM∥AB，则∠3=∠1，∠4=∠5，∠1=∠6，而∠1=∠2，于是3+∠4=∠5+∠6．

    试题解析：分别过E、F 点作CD的平行线EM、FN，如图

    ∵AB∥CD，

    ∴CD∥FN∥EM∥AB，

    ∴∠3=∠2，∠4=∠5，∠1=∠6，

    而∠1=∠2，

    ∴∠3+∠4=∠5+∠6，

    即∠BEF=∠EFC．

    【题型】解答题
    【结束】
    26

    【题目】(1)填空21－20＝2( )； 22－21＝2( ) ；23 －22＝2( )

    (2)请用字母表示第n个等式，并验证你的发现．

    (3)利用(2)中你的发现，求20＋21＋22＋23＋…＋22016＋22017的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

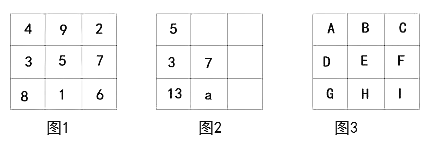
    【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。

    (1)如图2所示,求的值；

    (2)如图3所示:

    ①若求整式D；

    ②若求这九个整式的和是多少。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，定点A(－2，1)，点B在直线y＝x上，且横坐标为2，动点P在x轴上运动，当线段PA＋PB最短时，点P的坐标为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．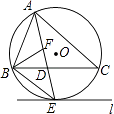

    （1）判断直线l与⊙O的位置关系，并说明理由；
    （2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；
    （3）在（2）的条件下，若DE=4，DF=3，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（ ）

    A.44°
    B.66°
    C.88°
    D.92°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为2的正方形ABCD内接于⊙O，点E是 上一点（不与A、B重合），点F是 上一点，连接OE，OF，分别与AB，BC交于点G，H，有下列结论：
    ① = ；
    ②△OGH是等腰三角形；
    ③四边形OGBH的面积随着点E位置的变化而变化；
    ④若BG=1﹣ ，则BG，GE， 围成的面积是 + ．
    其中正确的是（把所有正确结论的序号都填上）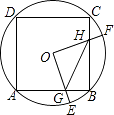

    查看答案和解析>>

    科目：初中数学 来源： 题型：

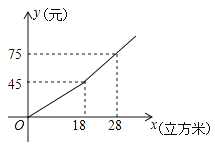
    【题目】某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准，该市的用户每月应交水费y（元）是用水量x（立方米）的函数，其图象如图所示．

    （1）若某月用水量为18立方米，则应交水费多少元？

    （2）求当x＞18时，y关于x的函数表达式，若小敏家某月交水费81元，则这个月用水量为多少立方米？

    查看答案和解析>>

    同步练习册答案