
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过点C作CB⊥x轴于点B.
=0,过点C作CB⊥x轴于点B.
(1)求A、C两点坐标;
(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.
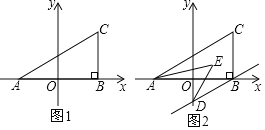
【答案】(1)A(﹣2,0),C(2,2);(2)∠AED的度数为45°.
【解析】
(1)根据偶次方和绝对值的非负性,可求得a、b的值,则A、C两点坐标可以求出;
(2)根据平行线的性质,得∠CAB+∠ODB=∠5+∠6=90°,再根据AE、DE分别平分∠CAB、∠ODB,得∠1=∠3=![]() ∠CAB,∠2=∠4=
∠CAB,∠2=∠4=![]() ∠ODB,最后根据∠AED=∠1+∠2可求得的度数.
∠ODB,最后根据∠AED=∠1+∠2可求得的度数.
(1)∵(a+2)2+![]() =0
=0
∴a+2=0,b﹣2=0,
∴a=﹣2,b=2,
∴A(﹣2,0),C(2,2);
(2)∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,
∴∠CAB+∠ODB=∠5+∠6=90°,
过点E作EF∥AC,如图
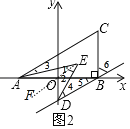
∵BD∥AC
∴BD∥EF∥AC,
∵AE、DE分别平分∠CAB、∠ODB,
∴∠1=∠3=![]() ∠CAB,∠2=∠4=
∠CAB,∠2=∠4=![]() ∠ODB,
∠ODB,
∴∠AED=∠1+∠2=![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
∴∠AED的度数为45°.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字 ![]() 、
、 ![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张的爸爸在上周星期六骑摩托车带小张和弟弟到离家27千米的游乐园玩耍,爸爸自己骑摩托车的速度为26千米![]() 时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米
时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米![]() 时,当天三人同时从家出发,弟弟以4千米
时,当天三人同时从家出发,弟弟以4千米![]() 时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、
时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、![]() 爸爸骑摩托车掉头和停放摩托车的时间忽略不计
爸爸骑摩托车掉头和停放摩托车的时间忽略不计![]() 问:小张搭乘摩托车的路程为______千米.
问:小张搭乘摩托车的路程为______千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,因为
的小数部分,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分又例如:因为
的整数部分是1,将这个数减去其整数部分,差就是小数部分又例如:因为![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,所以
<3,所以![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2)
﹣2)
请解答:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上
(1)求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;
(2)当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;
(3)抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )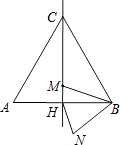
A.![]() a
a
B.a
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com