
【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )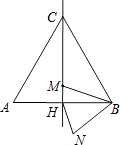
A.![]() a
a
B.a
C.![]()
D.![]()
【答案】D
【解析】解:如图,取BC的中点G,连接MG,
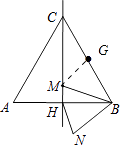
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB= ![]() AB,
AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,
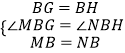 ,
,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,MG⊥CH时,MG最短,即HN最短,
此时∵∠BCH= ![]() ×60°=30°,CG=
×60°=30°,CG= ![]() AB=
AB= ![]() ×2a=a,
×2a=a,
∴MG= ![]() CG=
CG= ![]() ×a=
×a= ![]() ,
,
∴HN= ![]() ,
,
所以答案是:D.
【考点精析】通过灵活运用等边三角形的性质和含30度角的直角三角形,掌握等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )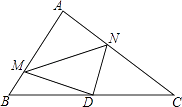
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
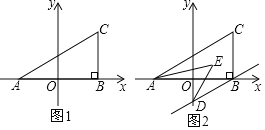
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过点C作CB⊥x轴于点B.
=0,过点C作CB⊥x轴于点B.
(1)求A、C两点坐标;
(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书本数相等.
(1)求去年购买的文学书和科普书的单价各是多少元?
(2)若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,为了普及科普知识,书店举办了每买三本科普书就赠一本文学书的优惠活动,这所中学今年计划在优惠活动期间,再购进文学书和科普书共200本,且购买文学书和科普书的总费用不超过1880元,这所中学今年最多能购进多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
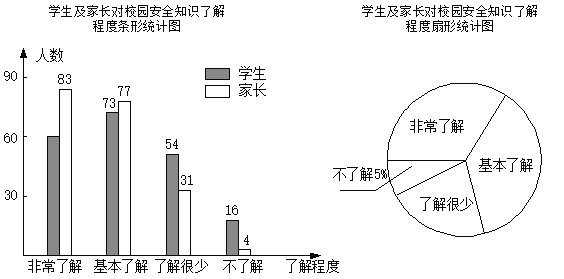
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
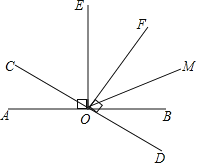
【题目】如图,已知直线AB与CD相交于点0,OE⊥AB,OF⊥CD,OM是∠BOF的角平分线
(1)若∠AOC=25°,求∠BOD和∠COE的度数.
(2)若∠AOC=a,求∠EOM的度数(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣3),C(﹣4,﹣1).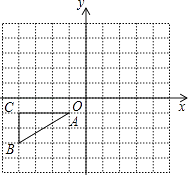
①作出△ABC关于原点O中心对称的图形;
②将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 , 画出△A1B1C1 , 并写出点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com