
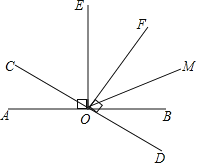
【题目】如图,已知直线AB与CD相交于点0,OE⊥AB,OF⊥CD,OM是∠BOF的角平分线
(1)若∠AOC=25°,求∠BOD和∠COE的度数.
(2)若∠AOC=a,求∠EOM的度数(用含a的代数式表示)
【答案】(1)∠COE =25°;(2)∠EOM=45°+![]() α.
α.
【解析】
(1)根据垂直的定义可知∠AOE=90°,根据对顶角相等可得∠BOD的度数,由∠COE=∠AOE-∠AOC计算,即可得出答案.
(2)根据对顶角相等可得∠BOD=∠AOC=α,由垂直的定义和角的运算可得∠BOF=90°-α,根据角平分线的定义得∠BOM=45°-![]() α,再由垂直定义即可求得答案.
α,再由垂直定义即可求得答案.
(1)解: ∵OE⊥AB,
∴∠AOE=90°,
又∵∠AOC=25°,
∴∠COE=∠AOE-∠AOC=90°-25°=65°,∠BOD=∠AOC=25°;
(2)解: ∵∠AOC=α,
∴∠BOD=∠AOC=α,
∵OF⊥CD,
∴∠DOF=90°,
∴∠BOF=∠DOF-∠DOB=90°-α,
又∵OM平分∠BOF,
∴∠BOM=![]() ∠BOF=
∠BOF=![]() (90°-α)=45°-
(90°-α)=45°-![]() α,
α,
∵OE⊥AB,
∴∠BOE=90°,
∴∠EOM=∠BOE-∠BOM,
=90°-(45°-![]() α),
α),
=45°+![]() α.
α.
故答案为:(1)∠BOD=25°∠COE =65°;(2)∠EOM=45°+![]() α.
α.


科目:初中数学 来源: 题型:
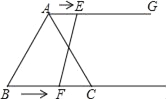
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上
(1)求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;
(2)当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;
(3)抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() )2018×(﹣
)2018×(﹣![]() )2019×(﹣1)2017;
)2019×(﹣1)2017;
(2)[(x﹣y)2+(x+y)(x﹣y)]÷2x;
(3)(x+2y﹣3)(x﹣2y+3);
(4)(1﹣![]() )÷
)÷![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )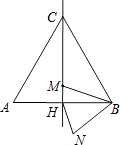
A.![]() a
a
B.a
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
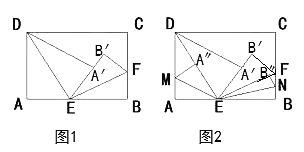
【题目】如图1,长方形ABCD沿着直线DE和EF折叠,使得AB的对应点![]() 和点E在同一条直线上。
和点E在同一条直线上。
(1)求∠DEF的度数;
(2)如图2,若再次沿着直线EM和EN折叠使得A、B的对应点![]() 分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
(1)建立适当的直角坐标系,并写出各个顶点的坐标;
(2)将(1)中各顶点的横坐标都加2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
(3)将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
(4)将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数y= ![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)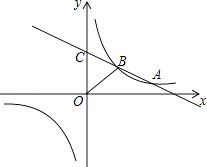
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是( )
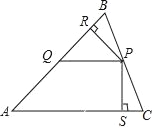
A. ②③④ B. ①② C. ①④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com