【题目】如图，在△ABC中，P是BC上的点，作PQ∥AC交AB于点Q，分别作PR⊥AB，PS⊥AC，垂足分别是R，S，若PR=PS，则下面三个结论：①AS=AR；②AQ=PQ；③△PQR≌△CPS；④AC﹣AQ=2SC，其中正确的是（ ）
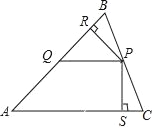
A. ②③④ B. ①② C. ①④ D. ①②③④
名校课堂系列答案科目：初中数学 来源： 题型：
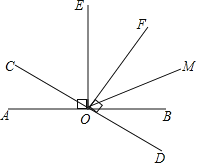
【题目】如图，已知直线AB与CD相交于点0，OE⊥AB，OF⊥CD，OM是∠BOF的角平分线
（1）若∠AOC=25°，求∠BOD和∠COE的度数．
（2）若∠AOC=a，求∠EOM的度数(用含a的代数式表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC，BD相交于点O，且OA=OC=4，OB=OD=6，P是线段BD上一动点，过点P作EF∥AC，与四边形的两条边分别交于点E，F，设BP=x，EF=y，则下列能表示y与x之间函数关系的图象是（ ）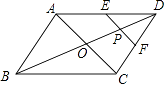
A.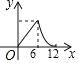
B.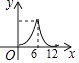
C.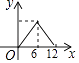
D.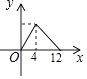
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某包装生产企业承接了一批上海世博会的礼品盒制作业务，为了确保质量，该企业进行试生产．他们购得规格是170cm×40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材．如图所示，（单位：cm）
（1）列出方程（组），求出图甲中a与b的值．
（2）在试生产阶段，若将m张标准板材用裁法一裁剪，n张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图乙横式无盖礼品盒．
①两种裁法共产生A型板材 张，B型板材 张（用m、n的代数式表示）；
②当30≤m≤40时，所裁得的A型板材和B型板材恰好用完，做成的横式无盖礼品盒可能是 个．（在横线上直接写出所有可能答案，无需书写过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，
，
，
，AD、BE相交于点M，连接CM．
求证：
；
求
的度数
用含
的式子表示
；
如图2，当
时，点P、Q分别为AD、BE的中点，分别连接CP、CQ、PQ，判断
的形状，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB＝30，∠AOB 内有一定点 P，且 OP＝12，在 OA 上有一动点 Q，OB 上有 一动点 R。若△PQR 周长最小，则最小周长是( )
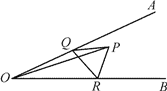
A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知BD∥AC，CE∥BA，且点D，A，E在一条直线上，设∠BAC＝x，∠D＋∠E＝y.
(1)试用含x的代数式表示y；
(2)当x＝90°时，判断直线DB与直线EC的位置关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
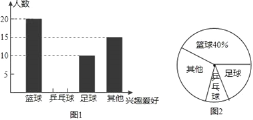
【题目】为响应国家要求中小学生每天锻炼1小时的号召，某校开展了形式多样的“阳光体育运动”活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了图1和图2的统计图．请回答下列问题：
（1）该班共有多少名学生？
（2）求图1中“乒乓球”部分的人数，并在图1中将“乒乓球”部分的图形补充完整；
（3）求出扇形统计图中表示“足球”的扇形的圆心角度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(11分)如图1，点A(a，b)在平面直角坐标系xOy中，点A到坐标轴的垂线段AB，AC与坐标轴围成矩形OBAC，当这个矩形的一组邻边长的和与积相等时，点A称作“垂点”，矩形称作“垂点矩形”.
(1)在点P(1，2)，Q(2，－2)，N(
，－1)中，是“垂点”的点为 ；
(2)点M(－4，m)是第三象限的“垂点”，直接写出m的值 ；
(3)如果“垂点矩形”的面积是
，且“垂点”位于第二象限，写出满足条件的“垂点”的坐标 ；
(4)如图2，平面直角坐标系的原点O是正方形DEFG的对角线的交点，当正方形DEFG的边上存在“垂点”时，GE的最小值为8.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
