
【题目】已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上
(1)求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;
(2)当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;
(3)抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
【答案】
(1)解:∵当x=1时,y=1﹣2a+2a+2=3,
∴抛物线C1必过定点A(1,3),
∵抛物线C1:y=x2﹣2ax+2a+2=(x﹣a)2﹣a 2+2a+2,
∴顶点P(a,﹣a 2+2a+2)
(2)解:∵yP=﹣a 2+2a+2=﹣(a﹣1)2+3≤3
∴当a=1时,P达到最高位置(1,3)
此时抛物线C1解析式为y=x2﹣2x+4,
∴y=x2﹣2x+4=(x﹣1)2+3≥3,
∵当m≤x≤n时恰有3m≤y≤3n,
∴3≤3m≤y≤3n,
∴1≤m≤n,
∴当1≤m≤x≤n,y随x的增大而增大,
∴当x=m时,y=3m,当x=n时,y=3n,
则 ![]() ,
,
解得: ![]() ,
,
∵1≤m≤n,
∴m=1、n=4;
(3)解:∵抛物线C1:y=x2﹣2ax+2a+2与y轴交于B点
∴B(0,2a+2)
∵函数yP=﹣x 2+2x+2图象C2与y轴交于C点
∴C(0,2)
∵A(1,3)
∴由勾股定理得AC= ![]() ,BC=|2a|,AB2=(2a﹣1)2+1
,BC=|2a|,AB2=(2a﹣1)2+1
∵△ABC为等腰三角形,
∴①AC=BC ②BC2=AB2 ③AC2=AB2
∴ ![]() =|2a|或4a2=(2a﹣1)2+1或2=(2a﹣1)2+1,
=|2a|或4a2=(2a﹣1)2+1或2=(2a﹣1)2+1,
∴ ![]() 或
或 ![]() 或a=1或a=0(B与C重合,舍去),
或a=1或a=0(B与C重合,舍去),
即a=± ![]() 或a=
或a= ![]() 或a=1
或a=1
【解析】(1)因为当x=1时,抛物线的值是3,所以抛物线C1必过定点A(1,3),用配方法写出抛物线的顶点式即可;(2)根据抛物线的顶点式得出P点达到最高位置的坐标,求出抛物线C1的解析式,通过分析讨论求出m、n的值;(3)由抛物线C1与y轴交于B点,得到B点坐标的表达式,由抛物线C2与y轴交于C点,得到C点坐标,根据勾股定理求出AC、BC、AB2的值,根据等腰三角形的性质,△ABC为等腰三角形求出a的值,此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )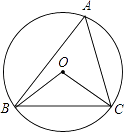
A.3 ![]()
B.4 ![]()
C.5 ![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: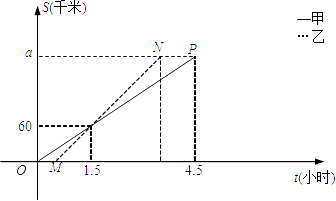
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
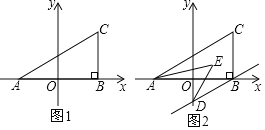
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过点C作CB⊥x轴于点B.
=0,过点C作CB⊥x轴于点B.
(1)求A、C两点坐标;
(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司准备购买机器人来代替人工分拣已知购买- 台甲型机器人比购买-台乙型机器人多![]() 万元;购买
万元;购买![]() 台甲型机器人和
台甲型机器人和![]() 台乙型机器人共需
台乙型机器人共需![]() 万元.
万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型、乙型机器人每台每小时分拣快递分别是![]() 件、
件、![]() 件,该公司计划最多用
件,该公司计划最多用![]() 万元购买
万元购买![]() 台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书本数相等.
(1)求去年购买的文学书和科普书的单价各是多少元?
(2)若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,为了普及科普知识,书店举办了每买三本科普书就赠一本文学书的优惠活动,这所中学今年计划在优惠活动期间,再购进文学书和科普书共200本,且购买文学书和科普书的总费用不超过1880元,这所中学今年最多能购进多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
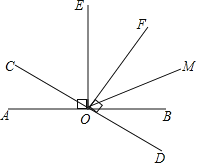
【题目】如图,已知直线AB与CD相交于点0,OE⊥AB,OF⊥CD,OM是∠BOF的角平分线
(1)若∠AOC=25°,求∠BOD和∠COE的度数.
(2)若∠AOC=a,求∠EOM的度数(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )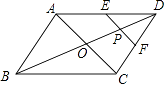
A.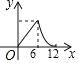
B.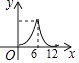
C.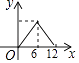
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com