
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
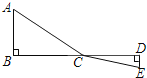
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)A、C、E三点共线;(3)13.
;(2)A、C、E三点共线;(3)13.
【解析】
(1)由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;
(2)若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小;
(3)由(1)(2)的结果可作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,则AE的长即为代数式![]() 的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.
的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.
解:(1)设CD=x,则BC=8-x,
∵AC=![]() ,CE=
,CE=![]() ,
,
∴AC+CE=![]() +
+![]() ;
;
(2)由两点之间线段最短可知,当A、C、E三点共线时,AC+CE的值最小;
(3)如右图所示

作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,设BC=x,则AE的长即为代数![]() 的最小值.
的最小值.
过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,
则AB=DF=2,AF=BD=12,EF=ED+DF=3+2=5,
所以AE=![]() =
=![]() =13,
=13,
即![]() 的最小值为13.
的最小值为13.


科目:初中数学 来源: 题型:
【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A.∠B=50° ,∠C=40°
B.∠B=∠C=45°
C.∠A,∠B,∠C的度数比为5:3:2
D.∠A-∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形两边中点的连线叫做这个三角形的中位线.只要顺次连结三角形三条中位线,则可将原三角形分割为四个全等的小三角形(如图(1));把三条边分成三等份,再按照图(2)将分点连起来,可以看作将整个三角形分成9个全等的小三角形;把三条边分成四等份,…,按照这种方式分下去,第n个图形中应该得到( )个全等的小三角形.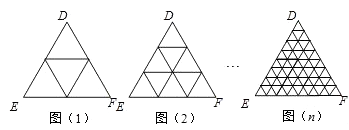
A.![]()
B.![]()
C.![]()
D.(n+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两个数也互为相反数”
(1)举一个具体的例子来判断上述结论是否成立;
(2)若![]() 和
和![]() 互为相反数,且x+5的平方根是它本身,求x+y的立方根.
互为相反数,且x+5的平方根是它本身,求x+y的立方根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com