
【题目】在等腰△ABC中,三边分别为a、b、c,其中 ![]() ,若关于x的方程
,若关于x的方程 ![]() 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
【答案】解:∵方程有两个相等的实数根,
∴△=b2-4ac=(b+2)2-4×1×(6-b)=0,
∴b2+8b-20=0,
∴(b+10)(b-2)=0
∴b1=-10,b2=2,
又∵b为等腰△ABC的边,
∴b=2,
又∵a=5,
∴a=c=5,
∴C△ABC=2+5+5=12.
故答案为:12.
【解析】根据一元二次方程根的判别式结合题意求出b的值,再根据等腰三角形的性质以及三角形三边的关系求出△ABC的周长.
【考点精析】本题主要考查了求根公式和三角形三边关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
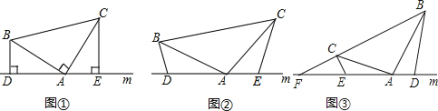
【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
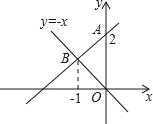
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
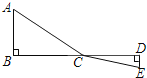
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com