
【题目】已知点P为平面内一点,若点P 到⊙O上的点的最长距离为5,最短距离为1,则⊙O 的半径为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.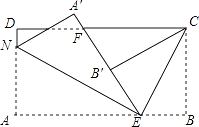
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
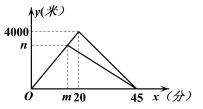
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )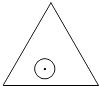
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形两边中点的连线叫做这个三角形的中位线.只要顺次连结三角形三条中位线,则可将原三角形分割为四个全等的小三角形(如图(1));把三条边分成三等份,再按照图(2)将分点连起来,可以看作将整个三角形分成9个全等的小三角形;把三条边分成四等份,…,按照这种方式分下去,第n个图形中应该得到( )个全等的小三角形.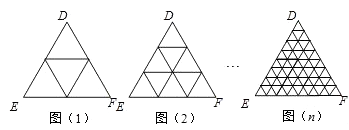
A.![]()
B.![]()
C.![]()
D.(n+1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com