
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )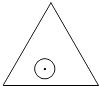
A.![]()
B.![]()
C.![]()
D.πr2
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】探究:如何把多项式x2+8x+15因式分解?
(1)观察:上式能否可直接利用完全平方公式进行因式分解? 答: ;
(阅读与理解):由多项式乘法,我们知道(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左地使用,即可对形如x2+(a+b)x+ab的多项式进行因式分解,即:
x2+(a+b)x+ab=(x+a)(x+b)
此类多项式x2+(a+b)x+ab的特征是二次项系数为1,常数项为两数之积,一次项系数为这两数之和.
(2)猜想并填空: x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )
(3)上面多项式x2+8x+15的因式分解是否正确,我们需要验证.请写出验证过程.
(4)请运用上述方法将下列多项式进行因式分解:
① x2+8x+12 ② x2-x-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

查看答案和解析>>
科目:初中数学 来源: 题型:
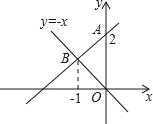
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
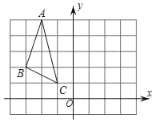
【题目】如图,△ABC在平面直角坐标系中,A(﹣2,5),B(﹣3,2),C(﹣1,1).
(1)请画出△ABC关于y轴的对称图形△A′B′C′,其中A点的对应点是A′,B点的对应点是B′,C点的对应点是C′,并写出A′,B′,C′三点的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
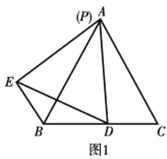
【题目】在等边三角形ABC中,AB=6,点D是BC边上的一点,点P是AB边上的一点,连接PD,以PD为边作等边三角形PDE,连接BE.
(1)如图1,当点P与点A重合时,
①找出图中的一对全等三角形,并证明;
②BE+BD=;
(2)如图2,若AP=1,请计算BE+BD的值.
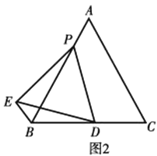
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com