
【题目】探究:如何把多项式x2+8x+15因式分解?
(1)观察:上式能否可直接利用完全平方公式进行因式分解? 答: ;
(阅读与理解):由多项式乘法,我们知道(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左地使用,即可对形如x2+(a+b)x+ab的多项式进行因式分解,即:
x2+(a+b)x+ab=(x+a)(x+b)
此类多项式x2+(a+b)x+ab的特征是二次项系数为1,常数项为两数之积,一次项系数为这两数之和.
(2)猜想并填空: x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )
(3)上面多项式x2+8x+15的因式分解是否正确,我们需要验证.请写出验证过程.
(4)请运用上述方法将下列多项式进行因式分解:
① x2+8x+12 ② x2-x-12
【答案】(1)不能;(2)3,5,3,5,3,5,(3)见解析;(4)①![]() ;②
;② ![]()
【解析】
(1)根据是否符合完全平方式的结构特征进行判断即可;
(2)根据“把一次项系数分解成两个数的和,并且这两个数的积等于常数项”进行填空即可;
(3)运用多项式乘以多项式进行验证即可;
(4)根据前面总结得出的分解因式方法,得出结果即可.
(1)∵x2+8x+15不是完全平方式,
∴x2+8x+15不能用完全平方公式进行因式分解.
故答案为:不能;
(2)∵8=5+3,15=5×3
∴x2+8x+15= x2+[( 3) +( 5 )]x + ( 3)×( 5)=(x+ 3 )(x+ 5 ),
故答案为:3,5,3,5,3,5,
(3)(x+3)(x+5)
=x2+3x+5x+15
= x2+8x+15;
(4)① x2+8x+12
= x2+(6+2)x+(6×2)
=(x+6)(x+2);
② x2-x-12
= x2+(3-4)x+[3×(-4)]
=(x-3)(x+4)


科目:初中数学 来源: 题型:
【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点D为直线BC上的一动点
,点D为直线BC上的一动点![]() 点D不与点B、C重合
点D不与点B、C重合![]() ,以AD为边作
,以AD为边作![]() ,使
,使![]() ,
,![]() ,连接CE.
,连接CE.
发现问题:
如图1,当点D在边BC上时,
![]() 请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
尝试探究:
![]() 如图2,当点D在边BC的延长线上且其他条件不变时,
如图2,当点D在边BC的延长线上且其他条件不变时,![]() 中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:
![]() 如图3,当点D在边CB的延长线上且其他条件不变时,若
如图3,当点D在边CB的延长线上且其他条件不变时,若![]() ,
,![]() ,求线段ED的长.
,求线段ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1 , △ABC与△A1B1C1成中心对称.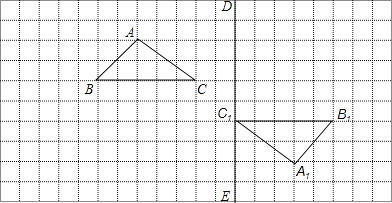
(1)画出△ABC和△A1B1C1的对称中心O;
(2)将△A1B1C1 , 沿直线ED方向向上平移6格,画出△A2B2C2;:
(3)将△A2B2C2绕点C2顺时针方向旋转90°,画出△A3B3C3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )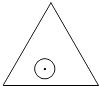
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com