
ЁОЬтФПЁПвбжЊ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуDЮЊжБЯпBCЩЯЕФвЛЖЏЕу
ЃЌЕуDЮЊжБЯпBCЩЯЕФвЛЖЏЕу![]() ЕуDВЛгыЕуBЁЂCжиКЯ
ЕуDВЛгыЕуBЁЂCжиКЯ![]() ЃЌвдADЮЊБпзї
ЃЌвдADЮЊБпзї![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌ
ЃЌ![]() ЃЌСЌНгCEЃЎ
ЃЌСЌНгCEЃЎ
ЗЂЯжЮЪЬтЃК
ШчЭМ1ЃЌЕБЕуDдкБпBCЩЯЪБЃЌ
![]() ЧыаДГіBDКЭCEжЎМфЕФЮЛжУЙиЯЕЮЊ______ЃЌВЂВТЯыBCКЭCEЁЂCDжЎМфЕФЪ§СПЙиЯЕЃК______ЃЎ
ЧыаДГіBDКЭCEжЎМфЕФЮЛжУЙиЯЕЮЊ______ЃЌВЂВТЯыBCКЭCEЁЂCDжЎМфЕФЪ§СПЙиЯЕЃК______ЃЎ
ГЂЪдЬНОПЃК
![]() ШчЭМ2ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌ
ШчЭМ2ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌ![]() жаBDКЭCEжЎМфЕФЮЛжУЙиЯЕЁЂBCКЭCEЁЂCDжЎМфЕФЪ§СПЙиЯЕЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыаДГіаТЕФЪ§СПЙиЯЕЃЌЫЕУїРэгЩЃЛ
жаBDКЭCEжЎМфЕФЮЛжУЙиЯЕЁЂBCКЭCEЁЂCDжЎМфЕФЪ§СПЙиЯЕЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыаДГіаТЕФЪ§СПЙиЯЕЃЌЫЕУїРэгЩЃЛ
ЭиеЙбгЩьЃК
![]() ШчЭМ3ЃЌЕБЕуDдкБпCBЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌШє
ШчЭМ3ЃЌЕБЕуDдкБпCBЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЯпЖЮEDЕФГЄЃЎ
ЃЌЧѓЯпЖЮEDЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ГЩСЂЃЌЪ§СПЙиЯЕВЛГЩСЂЃЌЙиЯЕЮЊBC=CE-CDЃЛЃЈ3ЃЉ
ГЩСЂЃЌЪ§СПЙиЯЕВЛГЩСЂЃЌЙиЯЕЮЊBC=CE-CDЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
![]() ИљОнЬѕМў
ИљОнЬѕМў![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌХаЖЈ
ЃЌХаЖЈ![]() Ёе
Ёе![]() ЃЌМДПЩЕУГіBDКЭCEжЎМфЕФЙиЯЕЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЃЌМДПЩЕУЕН
ЃЌМДПЩЕУГіBDКЭCEжЎМфЕФЙиЯЕЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЃЌМДПЩЕУЕН![]() ЃЛ
ЃЛ
![]() ИљОнвбжЊЬѕМўЃЌХаЖЈ
ИљОнвбжЊЬѕМўЃЌХаЖЈ![]() Ёе
Ёе![]() ЃЌЕУГі
ЃЌЕУГі![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЃЌМДПЩЕУЕН
ЃЌМДПЩЕУЕН![]() ЃЛ
ЃЛ
![]() ИљОнЬѕМўХаЖЈ
ИљОнЬѕМўХаЖЈ![]() Ёе
Ёе![]() ЃЌЕУГі
ЃЌЕУГі![]() ЃЌдк
ЃЌдк![]() жаЃЌгЩЙДЙЩЖЈРэЕУ
жаЃЌгЩЙДЙЩЖЈРэЕУ![]() ЃЌМДПЩНтОіЮЪЬт.
ЃЌМДПЩНтОіЮЪЬт.
![]() ШчЭМ1ЃЌ
ШчЭМ1ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
![]() Ёе
Ёе![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД![]() ЃЛ
ЃЛ
гЩ![]() ПЩЕУЃЌ
ПЩЕУЃЌ![]() Ёе
Ёе![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
![]() ГЩСЂЃЌЪ§СПЙиЯЕВЛГЩСЂЃЌЙиЯЕЮЊ
ГЩСЂЃЌЪ§СПЙиЯЕВЛГЩСЂЃЌЙиЯЕЮЊ![]() ЃЎ
ЃЎ
РэгЩЃКШчЭМ2жаЃЌгЩ![]() ЭЌРэПЩЕУЃЌ
ЭЌРэПЩЕУЃЌ
![]() ЃЌ
ЃЌ
Ёр![]()
МД![]() EЃЌ
EЃЌ
![]() дк
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
![]() Ёе
Ёе![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
![]() ШчЭМ3жаЃЌгЩ
ШчЭМ3жаЃЌгЩ![]() ЭЌРэПЩЕУЃЌ
ЭЌРэПЩЕУЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
взжЄ![]() Ёе
Ёе![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёп![]()
![]() ЃЌ
ЃЌ
дк![]() жаЃЌгЩЙДЙЩЖЈРэЕУ
жаЃЌгЩЙДЙЩЖЈРэЕУ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ


 зпНјЮФбдЮФЯЕСаД№АИ
зпНјЮФбдЮФЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁб ![]() ЕФдВаФ
ЕФдВаФ ![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§ ![]() ЕФЭМЯёЩЯЃЌЧвгы
ЕФЭМЯёЩЯЃЌЧвгы ![]() жсЁЂ
жсЁЂ ![]() жсЯрЧагкЕу
жсЯрЧагкЕу ![]() ЁЂ
ЁЂ ![]() ЃЌвЛДЮКЏЪ§
ЃЌвЛДЮКЏЪ§ ![]() ЕФЭМЯёОЙ§Еу
ЕФЭМЯёОЙ§Еу ![]() ЃЌЧвгы
ЃЌЧвгы ![]() жсНЛгкЕу
жсНЛгкЕу ![]() ЃЌгыЁб
ЃЌгыЁб ![]() ЕФСэвЛИіНЛЕуЮЊЕу
ЕФСэвЛИіНЛЕуЮЊЕу ![]() .
.
ЃЈ1ЃЉЧѓ ![]() ЕФжЕМАЕу
ЕФжЕМАЕу ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓ ![]() ГЄМА
ГЄМА ![]() ЕФДѓаЁЃЛ
ЕФДѓаЁЃЛ
ЃЈ3ЃЉШєНЋЁб ![]() би
би ![]() жсЩЯЯТЦНвЦЃЌЪЙЦфгы
жсЩЯЯТЦНвЦЃЌЪЙЦфгы ![]() жсМАжБЯп
жсМАжБЯп ![]() ОљЯрЧаЃЌЧѓЦНвЦЕФЗНЯђМАЦНвЦЕФОрРы.
ОљЯрЧаЃЌЧѓЦНвЦЕФЗНЯђМАЦНвЦЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
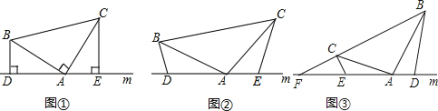
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌEЃЌFЃЌGЃЌHЗжБ№ЪЧБпABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЎШєЫФБпаЮEFGHЮЊСтаЮЃЌдђЖдНЧЯпACЁЂBDгІТњзуЬѕМў__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌДгAЕуЯђЁЯACBЕФНЧЦНЗжЯпзїДЙЯпЃЌДЙзуЮЊDЃЌEЪЧABЕФжаЕуЃЌвбжЊAC=4ЃЌBC=6ЃЌдђDEЕФГЄЮЊЃЈ ЃЉ
A.1
B.![]()
C.![]()
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈжЊЪЖЩњГЩЃЉЮвУЧвбОжЊЕРЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФУцЛ§ПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЎР§ШчЭМ1ПЩвдЕУЕНЃЈa+bЃЉ2ЃНa2+2ab+b2ЃЌЛљгкДЫЃЌЧыНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉИљОнЭМ2ЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕУЕНЕФНсТлЃЌНтОіЯТУцЕФЮЪЬтЃКШєa+b+cЃН10ЃЌab+ac+bcЃН35ЃЌдђa2+b2+c2ЃНЁЁ ЁЁЃЎ
ЃЈ3ЃЉаЁУїЭЌбЇгУЭМ3жаxеХБпГЄЮЊaЕФе§ЗНаЮЃЌyеХБпГЄЮЊbЕФе§ЗНаЮЃЌzеХПэЁЂГЄЗжБ№ЮЊaЁЂbЕФГЄЗНаЮжНЦЌЦДГівЛИіУцЛ§ЮЊЃЈ2a+bЃЉЃЈa+2bЃЉГЄЗНаЮЃЌдђx+y+zЃНЁЁ ЁЁЃЎ
ЃЈжЊЪЖЧЈвЦЃЉЃЈ4ЃЉЪТЪЕЩЯЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФЬхЛ§вВПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЌЭМ4БэЪОЕФЪЧвЛИіБпГЄЮЊxЕФе§ЗНЬхЭкШЅвЛИіаЁГЄЗНЬхКѓжиаТЦДГЩвЛИіаТГЄЗНЬхЃЌЧыФуИљОнЭМ4жаЭМаЮЕФБфЛЏЙиЯЕЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНОПЃКШчКЮАбЖрЯюЪНx2+8x+15вђЪНЗжНтЃП
ЃЈ1ЃЉЙлВьЃКЩЯЪНФмЗёПЩжБНгРћгУЭъШЋЦНЗНЙЋЪННјаавђЪНЗжНтЃП Д№ЃК ЃЛ
ЃЈдФЖСгыРэНтЃЉЃКгЩЖрЯюЪНГЫЗЈЃЌЮвУЧжЊЕР(x+a)(x+b)=x2+(a+b)x+abЃЌНЋИУЪНДггвЕНзѓЕиЪЙгУЃЌМДПЩЖдаЮШчx2+(a+b)x+abЕФЖрЯюЪННјаавђЪНЗжНтЃЌМДЃК
x2+(a+b)x+ab=(x+a)(x+b)
ДЫРрЖрЯюЪНx2+(a+b)x+abЕФЬиеїЪЧЖўДЮЯюЯЕЪ§ЮЊ1ЃЌГЃЪ§ЯюЮЊСНЪ§жЎЛ§ЃЌвЛДЮЯюЯЕЪ§ЮЊетСНЪ§жЎКЭЃЎ
ЃЈ2ЃЉВТЯыВЂЬюПеЃК x2+8x+15= x2+[( ) +( )]x + ( )ЁС( )=(x+ )(x+ )
ЃЈ3ЃЉЩЯУцЖрЯюЪНx2+8x+15ЕФвђЪНЗжНтЪЧЗёе§ШЗЃЌЮвУЧашвЊбщжЄЃЎЧыаДГібщжЄЙ§ГЬЃЎ
ЃЈ4ЃЉЧыдЫгУЩЯЪіЗНЗЈНЋЯТСаЖрЯюЪННјаавђЪНЗжНтЃК
Ђй x2+8x+12 Ђк x2-x-12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ШчЭМЂйЃЌвбжЊЃКRtЁїABCжаЃЌAB=ACЃЌжБЯпmОЙ§ЕуAЃЌBDЁЭmгкDЃЌCEЁЭmгкEЃЌЧѓжЄЃКDE=BD+CEЃЛ
(2)ШчЭМЂкЃЌНЋ(1)жаЕФЬѕМўИФЮЊЃКЁїABCжаЃЌAB=ACЃЌВЂЧвЁЯBDA=ЁЯAEC=ЁЯBAC=ІСЃЌІСЮЊШЮвтШёНЧЛђЖлНЧЃЌЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂЃПШчГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
(3)гІгУЃКШчЭМЂлЃЌдкЁїABCжаЃЌЁЯBACЪЧЖлНЧЃЌAB=ACЃЌЁЯBADЃОЁЯCAEЃЌЁЯBDA=ЁЯAEC=ЁЯBACЃЌжБЯпmгыBCЕФбгГЄЯпНЛгкЕуFЃЌШєBC=2CFЃЌЁїABCЕФУцЛ§ЪЧ12ЃЌЧѓЁїABDгыЁїCEFЕФУцЛ§жЎКЭЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЈ-5ЃЌ0ЃЉЃЌBЃЈ-3ЃЌ0ЃЉЃЌЕуCдкyжсЕФе§АыжсЩЯЃЌЁЯCBO=45ЁуЃЌCDЁЮABЃЎЁЯCDA=90ЁуЃЎЕуPДгЕуQЃЈ4ЃЌ0ЃЉГіЗЂЃЌбиxжсЯђзѓвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдЫЖЏЪБЪБМфtУыЃЎ
ЃЈ1ЃЉЧѓЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕБЁЯBCP=15ЁуЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉвдЕуPЮЊдВаФЃЌPCЮЊАыОЖЕФЁбPЫцЕуPЕФдЫЖЏЖјБфЛЏЃЌЕБЁбPгыЫФБпаЮABCDЕФБпЃЈЛђБпЫљдкЕФжБЯпЃЉЯрЧаЪБЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com