
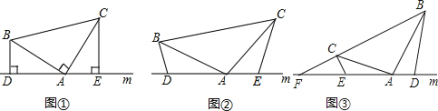
【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
【答案】(1)见解析; (2) 结论DE=BD+CE成立,理由见解析; (3)6
【解析】
(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,由AAS证得△ADB≌△CEA,则AE=BD,AD=CE,即可得出结论;
(2)由∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA即可得出答案;
(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ACF即可得出结果.
(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
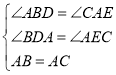
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2) 结论DE=BD+CE成立;理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,

∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3) ∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD,
在△ABD和△CEA中,

∴△ABD≌△CEA(AAS),
∴S△ABD=S△CEA,
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
∴S△ABC=![]() BCh=12,S△ACF=
BCh=12,S△ACF=![]() CFh,
CFh,
∵BC=2CF,
∴S△ACF=6,
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组![]()
现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点D为直线BC上的一动点
,点D为直线BC上的一动点![]() 点D不与点B、C重合
点D不与点B、C重合![]() ,以AD为边作
,以AD为边作![]() ,使
,使![]() ,
,![]() ,连接CE.
,连接CE.
发现问题:
如图1,当点D在边BC上时,
![]() 请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
尝试探究:
![]() 如图2,当点D在边BC的延长线上且其他条件不变时,
如图2,当点D在边BC的延长线上且其他条件不变时,![]() 中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:
![]() 如图3,当点D在边CB的延长线上且其他条件不变时,若
如图3,当点D在边CB的延长线上且其他条件不变时,若![]() ,
,![]() ,求线段ED的长.
,求线段ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
……
(1)根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是________ ;
(2)式子(n-1) n (n+1) (n+2)+1=___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.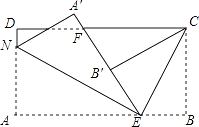
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A.∠B=50° ,∠C=40°
B.∠B=∠C=45°
C.∠A,∠B,∠C的度数比为5:3:2
D.∠A-∠B=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com