
【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A.∠B=50° ,∠C=40°
B.∠B=∠C=45°
C.∠A,∠B,∠C的度数比为5:3:2
D.∠A-∠B=90°
【答案】D
【解析】A.∵∠B=50° ,∠C=40° ,
∴∠B=180°-50°-40°=90°,
∴△ABC是直角三角形.A符合题意;
B.∵∠B=∠C=45° ,
∴∠A=180°-45°-45°=90°,
∴△ABC是直角三角形.B符合题意;
C.∵∠A,∠B,∠C的度数比为5:3:2 ,
设∠A=5x,∠B=3x,∠C=2x,
∴∠A+∠B+∠C=5x+3x+2x=180°,
∴x=18°,
∴∠A=90°,
∴△ABC是直角三角形.C符合题意;
D.∵∠A-∠B=90°,
∴∠A=90°+∠B![]() 90°,
90°,
∴△ABC是钝角三角形.D不符合题意;
所以答案是:D.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
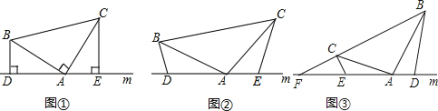
【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
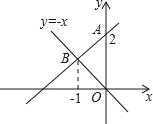
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
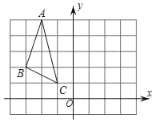
【题目】如图,△ABC在平面直角坐标系中,A(﹣2,5),B(﹣3,2),C(﹣1,1).
(1)请画出△ABC关于y轴的对称图形△A′B′C′,其中A点的对应点是A′,B点的对应点是B′,C点的对应点是C′,并写出A′,B′,C′三点的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )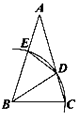
A.67.5°
B.52.5°
C.45°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
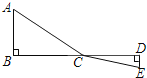
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com