Question

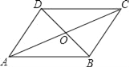
【题目】如图，AC与BD相交于点O，AB∥CD，AB＝CD，则图中的全等三角形共有（　　）

A. 1对B. 2对C. 3对D. 4对

Answer 1

【答案】D

【解析】

图中全等三角形有4对，是△ADB≌△CBD，△ABC≌△CDA，△AOD≌△COB，△AOB≌△COD．首先证明△AOB≌△COD（ASA），再利用全等三角形的性质和判定一一证明即可．

图中全等三角形有4对，是△ADB≌△CBD，△ABC≌△CDA，△AOD≌△COB，△AOB≌△COD，

理由是：∵AB∥CD，

∴∠ABD＝∠CDB，∠BAO＝∠DCO，

∵AB＝CD，

∴△AOB≌△COD（ASA），

∴OA＝OC，OB＝OD，

∵∠AOD＝∠COD，

∴△AOD≌△COB（SAS），

∴AD＝BC，

∵AD＝BC，CD＝AB，AC＝CA，

∴△ADC≌△CBA（SSS），

∵AD＝BC，AB＝CD，DB＝BD，

∴△ADB≌△CBD（SSS），

故选：D．