
【题目】有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
……
(1)根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是________ ;
(2)式子(n-1) n (n+1) (n+2)+1=___________ .
【答案】11881 ![]()
【解析】
(1)观察下列各式:1×2×3×4+1=52=(12+3×1+1)2,2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,4×5×6×7+1=292=(42+3×4+1)2,得出规律:n(n+1)(n+2)(n+3)+1=(n2+3n+1)2(n≥1),即可得出9×10×11×12+1的值.
(2)根据(1)得出的规律可得出结论.
(1)观察下列各式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
得出规律:n(n+1)(n+2)(n+3)+1=(n2+3n+1)2(n≥1)
所以9×10×11×12+1=(92+3×9+1)2=1092=11881
故答案为:11881
(2)根据(1)的结论得:
(n-1) n (n+1) (n+2)+1=[(n-1)2+3(n-1)+1]2=[n2-2n+1+3n-3+1]2=(n2+n-1)2
故答案为:(n2+n-1)2


科目:初中数学 来源: 题型:
【题目】在一个不透明的布口袋里装有白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀.
(1)随机地从袋中摸出1只球,则摸出白球的概率是多少?
(2)随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:

(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
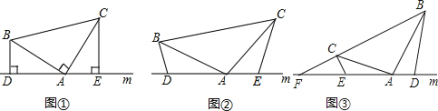
【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
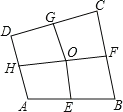
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com