
【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 . 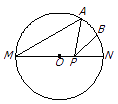
【答案】![]()
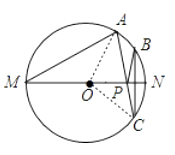
【解析】作点B关于MN的对称点C,连接AC交NM于点P,则P点就是所作的点;
∴PB=PC,
∴PA+PB=PA+PC=AC,
即此时PA+PB最小,
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数为60°,
又∵B为弧AN的中点,
∴弧BN的度数为30°,
又∵点B关于MN的对称点为C,
∴弧CN的度数为30°,
∴∠AOC=90°,
又∵MN是⊙O的直径,MN=2,
∴OA=OC=1,
∴AC=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】利用勾股定理的概念和圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,点A,B的坐标分别为(-2,0),(1,0).同时将点A ,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D,连接CD,AC, BD .
(1)写出点C , D 的坐标;
(2)在 y 轴上是否存在点E,连接EA ,EB,使S△EAB=S四边形ABDC?若存在,求出点E的坐标;若不存在,说明理由;
(3)点 P 是线段 AC 上的一个动点,连接 BP , DP ,当点 P 在线段 AC 上移动时(不与 A , C 重合),直接写出CDP 、ABP 与BPD 之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
……
(1)根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是________ ;
(2)式子(n-1) n (n+1) (n+2)+1=___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.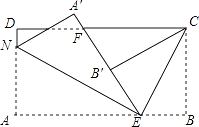
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。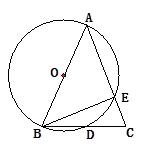
(1)求∠EBC的度数;
(2)求证:BD=CD。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到距离学校6千米的博物馆去参观,小磊准备乘出租车去,出租车的收费标准如下:3千米以下收费8元;3千米以上,每增加1千米,加收1.2元.
(1)写出出租车行驶的里程数![]() (
(![]() 大于3千米)与费用
大于3千米)与费用![]() (元)之间的关系式;
(元)之间的关系式;
(2)小磊只带10元钱,到博物馆够用吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com