
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
①将x=5,y=-1代入检验即可做出判断;
②将x和y分别用a表示出来,然后求出x+y=3来判断;
③将a=1代入方程组求出方程组的解,代入方程中检验即可;
④有x+y=3得到x、y都为自然数的解有4对.
①将x=5,y=-1代入方程组得:![]() ,
,
由①得a=2,由②得a=![]() ,故①不正确.
,故①不正确.
②解方程![]()
①-②得:8y=4-4a
解得:y=![]()
将y的值代入①得:x=![]() .
.
所以x+y=3,故无论a取何值,x、y的值都不可能互为相反数,故②正确.
③将a=1代入方程组得:![]() ,
,
解此方程得:![]() ,
,
将x=3,y=0代入方程x+y=3,方程左边=3=右边,是方程的解,故③正确.
④因为x+y=3,所以x、y都为自然数的解有![]() ,
,![]() ,
,![]() ,
,![]() .故④正确.
.故④正确.
则正确的选项有②③④.
故选B.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC的底边BC=13cm,D是腰AB上一点,且CD=12cm, BD=5cm.
(1)求证:△BDC是直角三角形;
(2)求△ABC的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.

(1)用两种不同的方法表示长方形ACDF的面积S
方法一:S=
方法二:S=
(2)求a,b,c之间的等量关系(需要化简)
(3)请直接运用(2)中的结论,求当c=5,a=3,S的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.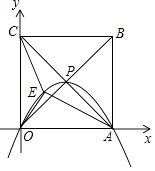
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感恩是中华民族的传统美德,在4月份某校提出了“感恩父母、感恩老师、感恩他人”的“三感”教育活动.感恩事例有:A.给父母过一次生日;B .为父母做一次家务活,让父母休息一天;C.给老师一个发自内心的拥抱,并且与老师谈心;D.帮助有困难的同学度过难关.为了解学生对这四种感恩事例的情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学在4种感恩事例中选择最想做的一种),将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了名学生;
(2)请补全扇形统计图中的数据及条形统计图;
(3)若有3名选 A的学生,1名选 C的学生组成志愿服务队外出参加联谊活动,欲从中随机选出2人担任活动负责人,请通过树状图或列表求两人均是选 A的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com