
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
【答案】(1)![]() ;(2)
;(2)![]() 时,最小值为-
时,最小值为-![]() ;(3)
;(3)![]() ,最小值为
,最小值为![]()
【解析】
(1)根据阅读材料,先将m24m5变形为m24m+49,再根据完全平方公式写成(m2)29,然后利用平方差公式分解即可;
(2)利用配方法将多项式![]() 转化为
转化为![]() ,然后利用非负数的性质进行解答;
,然后利用非负数的性质进行解答;
(3)利用配方法将多项式![]() 转化为
转化为![]() ,然后利用非负数的性质进行解答.
,然后利用非负数的性质进行解答.
(1)m24m5
=m24m+49
=(m2)29=
(m2+3)(m23)=
(m+1)(m5).
故答案为![]() ;
;
(2)![]()
=a24a+b2+6b+8
=a24a+4+b2+6b+9-5
=![]() ,
,
当a=2,b=3时,![]() 有最小值,最小值为-5;
有最小值,最小值为-5;
(3)∵![]()
=![]()
=![]()
=![]()
=![]()
∴当a=4,b=3时,多项式![]() 有最小值17.
有最小值17.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新药,在做药效试验时发现,如果成人按规定剂量服用,那么服药后,每毫升血液中含药量y(μg)随时间t(h)的变化图象如图所示,根据图象回答:
(1)服药后几时血液中含药量最高?每毫升血液中含多少微克?
(2)在服药几时内,每毫升血液中含药量逐渐升高?在服药几时后,每毫升血液中含药量逐渐下降?
(3)服药后14 h时,每毫升血液中含药量是多少微克?
(4)如果每毫升血液中含药量为4微克及以上时,治疗疾病有效,那么有效时间为几时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
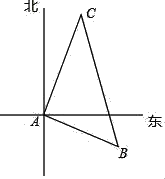
【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),在△ABC 中,∠BAC=70°,点 D 在 BC 的延长线上,三角形的内角∠ABC 与外角∠ACD 的角平分线 BP,CP 相交于点 P,求∠P 的度数.(写出完整的解答过程)




(感知):图(1)中,若∠BAC=m°,那么∠P= °(用含有 m 的代数式表示)
(探究):如图(2)在四边形 MNCB 中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD 的角平分线 BP,CP 相交于点 P.为了探究∠P 的度数与 α 和 β 的关系,小明同学想到将这个问题转化图(1)的模型,因此,他延长了边 BM 与 CN,设它们的交点为点 A, 如图( 3 ), 则∠ A= (用含有 α 和 β 的代数式表示), 因此∠P= .(用含有 α 和 β 的代数式表示)
(拓展):将(2)中的 α+β>180°改为 α+β<180°,四边形的内角∠MBC 与外角∠NCD 的角平分线所在的直线相交于点 P,其它条件不变,请直接写出∠P= .(用 α,β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.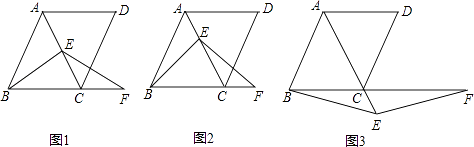
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE,EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com