
【题目】(1)如图(1),在△ABC 中,∠BAC=70°,点 D 在 BC 的延长线上,三角形的内角∠ABC 与外角∠ACD 的角平分线 BP,CP 相交于点 P,求∠P 的度数.(写出完整的解答过程)




(感知):图(1)中,若∠BAC=m°,那么∠P= °(用含有 m 的代数式表示)
(探究):如图(2)在四边形 MNCB 中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD 的角平分线 BP,CP 相交于点 P.为了探究∠P 的度数与 α 和 β 的关系,小明同学想到将这个问题转化图(1)的模型,因此,他延长了边 BM 与 CN,设它们的交点为点 A, 如图( 3 ), 则∠ A= (用含有 α 和 β 的代数式表示), 因此∠P= .(用含有 α 和 β 的代数式表示)
(拓展):将(2)中的 α+β>180°改为 α+β<180°,四边形的内角∠MBC 与外角∠NCD 的角平分线所在的直线相交于点 P,其它条件不变,请直接写出∠P= .(用 α,β的代数式表示)
【答案】(1)35°;感知:![]() m°,探究:α+β-180°,
m°,探究:α+β-180°,![]() (α+β)-90°;拓展:90°-
(α+β)-90°;拓展:90°-![]() α-
α-![]() β
β
【解析】
(1)根据角平分线的定义可得∠CBP=![]() ∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCP,然后整理即可得到∠P=
∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCP,然后整理即可得到∠P=![]() ∠A,代入数据计算即可得解.
∠A,代入数据计算即可得解.
[感知]求∠P度数的方法同(1)
[探究] 添加辅助线,利用(1)中结论解决问题即可;根据四边形的内角和定理表示出∠BCN,再表示出∠DCN,然后根据角平分线的定义可得∠PBC=![]() ∠ABC,∠PCD=∠DCN,三角形的一个外角等于与它不相邻的两个内角的和可得∠P+∠PBC=∠PCD,然后整理即可得解;
∠ABC,∠PCD=∠DCN,三角形的一个外角等于与它不相邻的两个内角的和可得∠P+∠PBC=∠PCD,然后整理即可得解;
拓展:同探究的思路求解即可
(1)∵BP平分∠ABC,
∴∠CBP=![]() ∠ABC,
∠ABC,
∵CP平分△ABC的外角,
∴∠DCP=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠A+
∠A+![]() ∠ABC,
∠ABC,
在△BCP中,由三角形的外角性质,∠DCP=∠CBP+∠P=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() ∠A+
∠A+![]() ∠ABC=
∠ABC=![]() ∠ABC+∠P,
∠ABC+∠P,
∴∠P=![]() ∠A=
∠A=![]() ×70°=35°.
×70°=35°.
感知:由(1)知∠P=![]() ∠A
∠A
∵∠BAC=m°,
∴∠P=![]() m°,
m°,
故答案为:![]() m°,
m°,
探究:延长BM交CN的延长线于A.
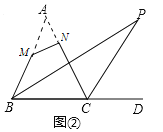
∵∠A=180°-∠AMN-∠ANM=180°-(180°-α)-(180°-β)=α+β-180°,
由(1)可知:∠P=![]() ∠A,
∠A,
∴∠P=![]() (α+β)-90°;
(α+β)-90°;
故答案为:α+β-180°,![]() (α+β)-90°;
(α+β)-90°;
[拓展] 如图③,延长MB交NC的延长线于A.
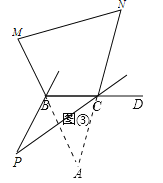
∵∠A=180°-α-β,∠P=![]() ∠A,
∠A,
∴∠P=![]() (180°-α-β)=90°-
(180°-α-β)=90°-![]() α-
α-![]() β
β
故答案为:90°-![]() α-
α-![]() β
β


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列说法中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF.正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识链接)斐波那契(约 1170﹣1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第 n(n 为正整数)个数 an 可表示为![]() .
.
(知识运用)计算第一个数 a1 和第二个数 a2;
(探究证明)证明连续三个数之间 an﹣1,an,an+1 存在以下关系:an+1﹣an=an﹣1(n≥2).
(探究拓展)根据上面的关系,请写出斐波那契数列中的前 8 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,分别延长边AB、BC、CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
(1)请你用直尺和圆规在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(﹣2,﹣1),则点C的坐标为;
(3)线段AB在旋转到线段AC的过程中,线段AB扫过区域的面积为
(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个圆锥的侧面,则该圆锥底面圆的半径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移3个单位长度再向下平移2个单位长度,画出两次平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕C1逆时针旋转90°,画出旋转后的△A2B2C1 , 求△A1B1C1旋转过程中扫过的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:
①4ac<b2;②a+c>b;③2a+b>0.
其中正确的有( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com