[题目]二次函数y=ax2+bx+c的图象如图所示.下列结论:①4ac＜b2,②a+c＞b,③2a+b＞0．其中正确的有( )A.①②B.①③C.②③D.①②③ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】二次函数y=ax2+bx+c的图象如图所示，下列结论：
①4ac＜b2；②a+c＞b；③2a+b＞0．
其中正确的有（）

A.①②
B.①③
C.②③
D.①②③

【答案】B
【解析】∵抛物线与x轴有两个交点，

∴△＞0，

∴b2﹣4ac＞0，

∴4ac＜b2，故①正确，

∵x=﹣1时，y＜0，

∴a﹣b+c＜0，

∴a+c＜b，故②错误，

∴对称轴x＞1，a＜0，

∴﹣ ＞1，

∴﹣b＜2a，

∴2a+b＞0，故③正确．

所以答案是：B．

【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】（1）如图（1），在△ABC 中，∠BAC=70°，点 D 在 BC 的延长线上，三角形的内角∠ABC 与外角∠ACD 的角平分线 BP，CP 相交于点 P，求∠P 的度数.（写出完整的解答过程）

（感知）：图（1）中，若∠BAC=m°，那么∠P= °（用含有 m 的代数式表示）

（探究）：如图（2）在四边形 MNCB 中，设∠M=α，∠N＝β，α+β＞180°，四边形的内角∠MBC与外角∠NCD 的角平分线 BP，CP 相交于点 P.为了探究∠P 的度数与 α 和 β 的关系，小明同学想到将这个问题转化图（1）的模型，因此，他延长了边 BM 与 CN，设它们的交点为点 A，如图（ 3 ），则∠ A= （用含有 α 和 β 的代数式表示），因此∠P= ．（用含有 α 和 β 的代数式表示）

（拓展）：将（2）中的 α+β＞180°改为 α+β＜180°，四边形的内角∠MBC 与外角∠NCD 的角平分线所在的直线相交于点 P，其它条件不变，请直接写出∠P＝　　．（用 α，β的代数式表示）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在菱形ABCD中，∠ABC=60°，E是对角线AC上一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．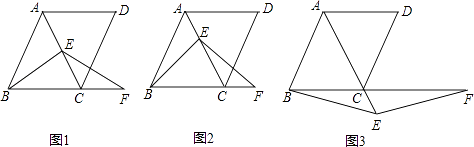

（1）若E是线段AC的中点，如图1，易证：BE=EF（不需证明）；
（2）若E是线段AC或AC延长线上的任意一点，其它条件不变，如图2、图3，线段BE，EF有怎样的数量关系，直接写出你的猜想；并选择一种情况给予证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】朗读者自开播以来，以其厚重的文化底蕴和感人的人文情怀，感动了数以亿计的观众，岳池县某中学开展“朗读”比赛活动，九年级、班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩满分为100分如图所示．

	平均数	中位数	众数
九班	85		85
九班		80

根据图示填写表格；

结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；

如果规定成绩较稳定班级胜出，你认为哪个班级能胜出？说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量yA（千克）与时间x（时）的函数图象，线段EF表示B种机器人的搬运量yB（千克）与时间x（时）的函数图象．根据图象提供的信息，解答下列问题：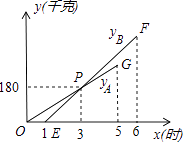

（1）求yB关于x的函数解析式；
（2）如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】2015年1月，市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价．评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查，了解他们每天在课外用于学习的时间，并绘制成如下不完整的统计图．

根据上述信息，解答下列问题：
（1）本次抽取的学生人数是；扇形统计图中的圆心角α等于；补全统计直方图；
（2）被抽取的学生还要进行一次50米跑测试，每5人一组进行．在随机分组时，小红、小花两名女生被分到同一个小组，请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率．