
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.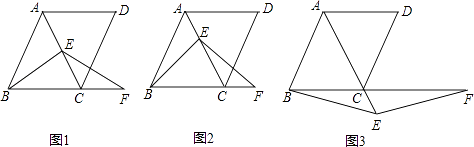
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE,EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
【答案】
(1)证明:∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵E是线段AC的中点,
∴∠CBE= ![]() ∠ABC=30°,AE=CE,
∠ABC=30°,AE=CE,
∵AE=CF,
∴CE=CF,
∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,
∴∠F=30°,
∴∠CBE=∠F,
∴BE=EF
(2)证明:图2:BE=EF.

图2证明如下:过点E作EG∥BC,交AB于点G,
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴△BGE≌△ECF(SAS),
∴BE=EF;
图3:BE=EF.
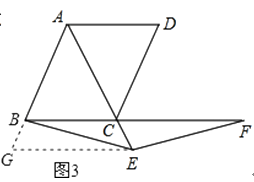
图3证明如下:过点E作EG∥BC交AB延长线于点G,
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴△BGE≌△ECF(SAS),
∴BE=EF
【解析】(1)根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,再求得CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角的性质求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证得BE=EF;
(2)图2,通过作辅助线,根据菱形的性质可得△ABC是等边三角形,根据等边三角形的性质得到AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠BGE=∠ECF=120°,然后利用“边角边”证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证BE=EF;
图3,证明思路与方法与图2完全相同.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
(1)请你用直尺和圆规在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(﹣2,﹣1),则点C的坐标为;
(3)线段AB在旋转到线段AC的过程中,线段AB扫过区域的面积为
(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个圆锥的侧面,则该圆锥底面圆的半径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移3个单位长度再向下平移2个单位长度,画出两次平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕C1逆时针旋转90°,画出旋转后的△A2B2C1 , 求△A1B1C1旋转过程中扫过的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
(1)求证:DF=EF;
(2)如果AD=2,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2),![]() ,C(﹣1,5)是“垂距点”是 ;
,C(﹣1,5)是“垂距点”是 ;
(2)若![]() 是“垂距点”,求m的值.
是“垂距点”,求m的值.
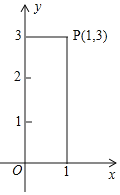
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:
①4ac<b2;②a+c>b;③2a+b>0.
其中正确的有( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com