
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
【答案】(1)∠AOC的度数为120°;(2)PD=![]() ,PD的最大值为
,PD的最大值为![]() ;(3)α=100,β=145.
;(3)α=100,β=145.
【解析】
(1)根据三角形内角和求得∠PAC+∠PCA的度数,然后根据角平分线的定义求得∠OAC+∠OCA的度数,从而求解;
(2)在△ABC中,当AP⊥BC时,AP最小,PD最大,由面积法求出AP的长,即可求出PD的最大值;
(3)如图,由已知可推出∠BAC=90°,设∠BAP=y,则∠PAC=90°-y,∠PCA=70°,
推出∠AOC=![]() y+100°,,因为0°<y<90°,可推出100°<∠AOC<145°,即可写出α、β的值.
y+100°,,因为0°<y<90°,可推出100°<∠AOC<145°,即可写出α、β的值.
解:在△APC中,∠PAC+∠PCA=180°-∠APC=120°
又∵OA、OC分别是∠PAC和∠PCA的角平分线
∴∠OAC+∠OCA=![]() ∠PAC+
∠PAC+![]() ∠PCA=
∠PCA=![]() (∠PAC+∠PCA)=60°
(∠PAC+∠PCA)=60°
∴在△OAC中,∠AOC=180°-60°=120°
(2)∵AD=AB=4,而PD=AD-AP=4-AP=4-x,
∴当AP⊥BC时,AP最小,PD最大,
此时,S△ABC=![]() BCAP=
BCAP=![]() ABAC,
ABAC,
即![]() ×5x=
×5x=![]() ×4×3,
×4×3,
解得,x=![]() ,
,
∴PD=![]() ,PD的最大值为:4-
,PD的最大值为:4-![]() =
=![]() ;
;
(3)如图,
![]()
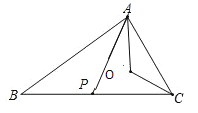
∵AB⊥AC,
∴∠BAC=90°,
设∠BAP=y,则∠PAC=90°-y,∠PCA=70°,
∵OA、OC分别是∠PAC和∠PCA的角平分线,
∴∠OAC=![]() ∠PAC,∠OCA=/span>
∠PAC,∠OCA=/span>![]() ∠PCA,
∠PCA,
∴∠AOC=180°-(∠OAC+∠OCA)
=180°-![]() (∠PAC+∠PCA)
(∠PAC+∠PCA)
=180°-![]() (90°-y+70°)
(90°-y+70°)
=![]() y+100°,
y+100°,
∵0°<y<90°,
∴100°<![]() y+100°<145°,
y+100°<145°,
即100°<∠AOC<145°,
∴α=100,β=145.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:

(1)根据图中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: ;
方法2: .
(2)从中你能发现什么结论,请用等式表示出来: ;
(3)利用(2)中结论解决下面的问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.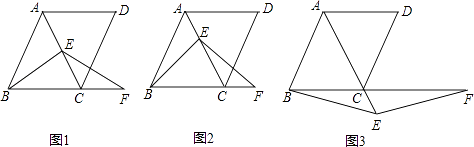
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE,EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数 ![]() (x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
A.2
B.﹣2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: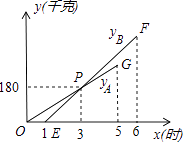
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com