
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx﹣ ![]() (a≠0)经过点A(1,0)和B(﹣3,0).
(a≠0)经过点A(1,0)和B(﹣3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标.
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2 , 此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的上方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标.
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:①tan∠ENM的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.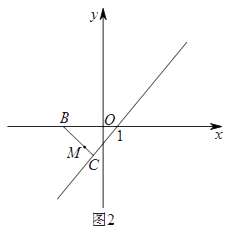
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列说法中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF.正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,BD为∠ABC的角平分线,DE、DF分别是∠ADB和∠ADC的角平分线,且∠BDF=α,则∠A与∠C的等量关系是________________(等式中含有α)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.

(1)用两种不同的方法表示长方形ACDF的面积S
方法一:S=
方法二:S=
(2)求a,b,c之间的等量关系(需要化简)
(3)请直接运用(2)中的结论,求当c=5,a=3,S的值
查看答案和解析>>
科目:初中数学 来源: 题型:
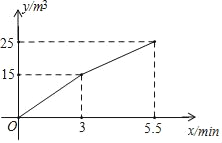
【题目】某种水泥储存罐的容量为25m3,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3min后,再打开输出口,匀速向运输车输出水泥,又经过2.5min水泥储存罐注满.已知水泥储存罐内的水泥量y(m3)与时间x(min)之间的函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量;
(2)当3≤x≤5.5时,求y与x之间的函数关系式;
(3)水泥储存罐每分钟向运输车输出的水泥量是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识链接)斐波那契(约 1170﹣1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第 n(n 为正整数)个数 an 可表示为![]() .
.
(知识运用)计算第一个数 a1 和第二个数 a2;
(探究证明)证明连续三个数之间 an﹣1,an,an+1 存在以下关系:an+1﹣an=an﹣1(n≥2).
(探究拓展)根据上面的关系,请写出斐波那契数列中的前 8 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移3个单位长度再向下平移2个单位长度,画出两次平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕C1逆时针旋转90°,画出旋转后的△A2B2C1 , 求△A1B1C1旋转过程中扫过的面积(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com