
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏC1ΘΚy=ax2+bx©¹ ![]() Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆBΘ®©¹3Θ§0Θ©Θ°
Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆBΘ®©¹3Θ§0Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏC1ΒΡΫβΈω ΫΘ§≤Δ–¥≥ωΤδΕΞΒψCΒΡΉχ±ξΘ°
Θ®2Θ©»γΆΦ1Θ§Α―≈ΉΈοœΏC1―ΊΉ≈÷±œΏACΖΫœρΤΫ“ΤΒΫΡ≥¥Π ±ΒΟΒΫ≈ΉΈοœΏC2 Θ§ ¥Υ ±ΒψAΘ§CΖ÷±πΤΫ“ΤΒΫΒψDΘ§E¥ΠΘ°…ηΒψF‘Ύ≈ΉΈοœΏC1…œ«“‘Ύx÷αΒΡ…œΖΫΘ§»τΓςDEF «“‘EFΈΣΒΉΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«σΒψFΒΡΉχ±ξΘ°
Θ®3Θ©»γΆΦ2Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§…ηΒψM «œΏΕΈBC…œ“ΜΕ·ΒψΘ§ENΓΆEMΫΜ÷±œΏBF”ΎΒψNΘ§ΒψPΈΣœΏΕΈMNΒΡ÷–ΒψΘ§Β±ΒψM¥”ΒψBœρΒψC‘ΥΕ· ±ΘΚΔΌtanΓœENMΒΡ÷Β»γΚΈ±δΜ·ΘΩ«κΥΒΟςάμ”…ΘΜΔΎΒψMΒΫ¥οΒψC ±Θ§÷±Ϋ”–¥≥ωΒψPΨ≠ΙΐΒΡ¬ΖœΏ≥ΛΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚΓΏ≈ΉΈοœΏC1ΘΚy=ax2+bx©¹ ![]() Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆBΘ®©¹3Θ§0Θ©Θ§
Θ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®1Θ§0Θ©ΚΆBΘ®©¹3Θ§0Θ©Θ§
Γύ  ΫβΒΟ
ΫβΒΟ ![]() Θ§
Θ§
Γύ≈ΉΈοœΏC1ΒΡΫβΈω ΫΈΣy= ![]() x2+x©¹
x2+x©¹ ![]() Θ§
Θ§
ΓΏy= ![]() x2+x©¹
x2+x©¹ ![]() =
= ![]() Θ®x+1Θ©2©¹2Θ§
Θ®x+1Θ©2©¹2Θ§
ΓύΕΞΒψCΒΡΉχ±ξΈΣΘ®©¹1Θ§©¹2Θ©ΘΜ
Θ®2Θ©ΫβΘΚ»γΆΦ1Θ§ΉςCHΓΆx÷α”ΎHΘ§
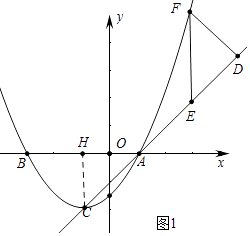
ΓΏAΘ®1Θ§0Θ©Θ§CΘ®©¹1Θ§©¹2Θ©Θ§
ΓύAH=CH=2Θ§
ΓύΓœCAB=ΓœACH=45ΓψΘ§
Γύ÷±œΏACΒΡΫβΈω ΫΈΣy=x©¹1Θ§
ΓΏΓςDEF «“‘EFΈΣΒΉΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœDEF=45ΓψΘ§
ΓύΓœDEF=ΓœACHΘ§
ΓύEFΓΈy÷αΘ§
ΓΏDE=AC=2 ![]() Θ§
Θ§
ΓύEF=4Θ§
…ηFΘ®mΘ§ ![]() m2+m©¹
m2+m©¹ ![]() Θ©Θ§‘ρEΘ®mΘ§m©¹1Θ©Θ§
Θ©Θ§‘ρEΘ®mΘ§m©¹1Θ©Θ§
ΓύΘ®©¹ ![]() m2+m©¹
m2+m©¹ ![]() Θ©©¹Θ®m©¹1Θ©=4Θ§
Θ©©¹Θ®m©¹1Θ©=4Θ§
ΫβΒΟm=©¹3Θ®…αΘ©Μρm=3Θ§
ΓύFΘ®3Θ§6Θ©ΘΜ
Θ®3Θ©ΫβΘΚΔΌtanΓœENMΒΡ÷ΒΈΣΕ®÷ΒΘ§≤ΜΖΔ…ζ±δΜ·ΘΜ
»γΆΦ2÷–Θ§ΉςEGΓΆACΘ§ΫΜBF”ΎGΘ§
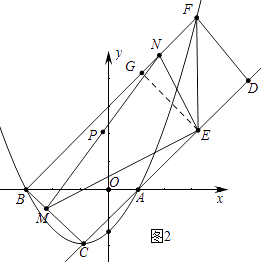
ÿDFâACȧBCâACȧ
ΓύDFΓΈBCΘ§
ÿDF=BC=ACȧ
ΓύΥΡ±Ώ–ΈDFBC «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΓœCDF=90ΓψΘ§
ΓύΥΡ±Ώ–ΈDFBC «ΨΊ–ΈΘ§
ΓύEG=BC=AC=2 ![]() Θ§
Θ§
ÿENâEMȧ
ΓύΓœMEN=90ΓψΘ§
ΓΏΓœCEG=90ΓψΘ§
ΓύΓœCEM=ΓœNEGΘ§
ΓύΓςENGΓΉΓςEMCΘ§
Γύ ![]() =
= ![]() Θ§
Θ§
ΓΏFΘ®3Θ§6Θ©Θ§EF=4Θ§
ΓύEΘ®3Θ§2Θ©Θ§
ΓΏCΘ®©¹1Θ§©¹2Θ©Θ§
ΓύEC=4 ![]() Θ§
Θ§
Γύ ![]() =
= ![]() =2Θ§
=2Θ§
ΓύtanΓœENM= ![]() =2ΘΜ
=2ΘΜ
ΓΏtanΓœENMΒΡ÷ΒΈΣΕ®÷ΒΘ§≤ΜΖΔ…ζ±δΜ·ΘΜ
ΔΎ»γΆΦ3©¹1÷–Θ§
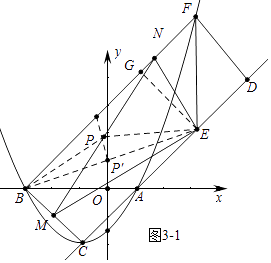
ΓΏ÷±Ϋ«»ΐΫ«–ΈEMN÷–Θ§PE= ![]() MNΘ§÷±Ϋ«»ΐΫ«–ΈBMN÷–Θ§PB=
MNΘ§÷±Ϋ«»ΐΫ«–ΈBMN÷–Θ§PB= ![]() MNΘ§
MNȧ
ΓύPE=PBΘ§
ΓύΒψP‘ΎEBΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
ΓύΒψPΨ≠ΙΐΒΡ¬ΖΨΕ «œΏΕΈPPΓδΘ§»γΆΦ3©¹2Θ§
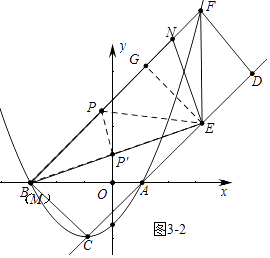
Β±ΒψM”κB÷ΊΚœ ±Θ§
ΓΏΓςEGNΓΉΓςECBΘ§
Γύ ![]() =
= ![]() Θ§
Θ§
ΓΏEC=4 ![]() Θ§EG=BC=2
Θ§EG=BC=2 ![]() Θ§
Θ§
ΓύEB=2 ![]() Θ§
Θ§
Γύ ![]() =
= ![]() Θ§
Θ§
ΓύEN= ![]() Θ§
Θ§
ΓΏP1P2 «ΓςBENΒΡ÷–ΈΜœΏΘ§
ΓύP1P2= ![]() EN=
EN= ![]() ΘΜ
ΘΜ
ΓύΒψMΒΫ¥οΒψC ±Θ§ΒψPΨ≠ΙΐΒΡ¬ΖœΏ≥ΛΈΣ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…«σΒΟΫβΈω ΫΘ§Α―ΫβΈω ΫΜ·ΈΣΕΞΒψ ΫΦ¥Ω…«σΒΟΕΞΒψΉχ±ξΘΜΘ®2Θ©ΗυΨίAΓΔCΒψΒΡΉχ±ξ«σΒΟ÷±œΏACΒΡΫβΈω ΫΈΣy=x©¹1Θ§ΗυΨίΧβ“βΒΡEF=4Θ§«σΒΟEFΓΈy÷αΘ§…ηFΘ®mΘ§ ![]() m2+m©¹
m2+m©¹ ![]() Θ©Θ§‘ρEΘ®mΘ§m©¹1Θ©Θ§¥”ΕχΒΟ≥ωΘ®©¹
Θ©Θ§‘ρEΘ®mΘ§m©¹1Θ©Θ§¥”ΕχΒΟ≥ωΘ®©¹ ![]() m2+m©¹
m2+m©¹ ![]() Θ©©¹Θ®m©¹1Θ©=4Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟFΒΡΉχ±ξΘΜΘ®3Θ©œ»«σΒΟΥΡ±Ώ–ΈDFBC «ΤΫ––ΨΊ–ΈΘ§ΉςEGΓΆACΘ§ΫΜBF”ΎGΘ§»ΜΚσ≈–Εœ≥ωΓςENGΓΉΓςEMCΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ε‘”Π±Ώ≥…±»άΐΦ¥Ω…«σΒΟtanΓœENMΒΡ÷ΒΘ§ΔΎ Ήœ»÷ΛΟςΒψP‘ΎEBΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§ΆΤ≥ωΒψPΨ≠ΙΐΒΡ¬ΖΨΕ «œΏΕΈPPΘ§Β±ΒψM”κB÷ΊΚœ ±Θ§ΗυΨίΙ¥Ι…Ε®άμΚΆ»ΐΫ«–ΈœύΥΤ«σΒΟENΘ§»ΜΚσΗυΨί»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΦ¥Ω…«σΒΟΓΘ
Θ©©¹Θ®m©¹1Θ©=4Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟFΒΡΉχ±ξΘΜΘ®3Θ©œ»«σΒΟΥΡ±Ώ–ΈDFBC «ΤΫ––ΨΊ–ΈΘ§ΉςEGΓΆACΘ§ΫΜBF”ΎGΘ§»ΜΚσ≈–Εœ≥ωΓςENGΓΉΓςEMCΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ε‘”Π±Ώ≥…±»άΐΦ¥Ω…«σΒΟtanΓœENMΒΡ÷ΒΘ§ΔΎ Ήœ»÷ΛΟςΒψP‘ΎEBΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§ΆΤ≥ωΒψPΨ≠ΙΐΒΡ¬ΖΨΕ «œΏΕΈPPΘ§Β±ΒψM”κB÷ΊΚœ ±Θ§ΗυΨίΙ¥Ι…Ε®άμΚΆ»ΐΫ«–ΈœύΥΤ«σΒΟENΘ§»ΜΚσΗυΨί»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΦ¥Ω…«σΒΟΓΘ


 ΗΏ÷–±ΊΥΔΧβœΒΝ–¥πΑΗ
ΗΏ÷–±ΊΥΔΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœC=90ΓψΘ§BC=8cmΘ§AC=6cmΘ§ΒψE «BCΒΡ÷–ΒψΘ§Ε·ΒψP¥”AΒψ≥ωΖΔ“‘ΟΩΟκ2cmΒΡΥΌΕ»―ΊAΓζCΓζB‘ΥΕ·Θ§…ηΒψP‘ΥΕ·ΒΡ ±Φδ «tΟκȧѫϥ±t=____Θ§ΓςAPEΒΡΟφΜΐΒ»”Ύ6Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΧνΩ’Άξ≥…ΆΤάμΙΐ≥ΧΘΚ
»γΆΦΘ§BCEΘ§AFE «÷±œΏΘ§ABΓΈCDΘ§Γœ1=Γœ2Θ§Γœ3=Γœ4Θ§«σ÷ΛADΓΈBEΘ°

÷ΛΟςΘΚΓΏABΓΈCDΘ®“―÷ΣΘ©
ΓύΓœ4=ΓœBAEΘ®ΓΓ Θ©
ΓΏΓœ3=Γœ4Θ®“―÷ΣΘ©
ΓύΓœ3=ΓœΓΓ ΓΓΘ®Β»ΝΩ¥ζΜΜΘ©
ΓΏΓœ1=Γœ2Θ®“―÷ΣΘ©
ΓύΓœ1+ΓœCAF=Γœ2+ΓœCAFΘ®ΓΓΓΓΘ©
Φ¥ΓœBAF=ΓœCAD
ΓύΓœ3=ΓœΓΓ ΓΓΘ®Β»ΝΩ¥ζΜΜΘ©
ΓύADΓΈBEΘ®ΓΓΓΓΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γ ‘œζ“Μ÷÷≥…±ΨΈΣΟΩΦΰ60‘ΣΒΡΖΰΉΑΘ§ΙφΕ® ‘œζΤΎΦδœζ έΒΞΦέ≤ΜΒΆ”Ύ≥…±ΨΒΞΦέΘ§«“Μώάϊ≤ΜΒΟΗΏ”Ύ50%Θ§Ψ≠ ‘œζΖΔœ÷Θ§œζ έΝΩyΘ®ΦΰΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©ΖϊΚœ“Μ¥ΈΚ· ΐy=kx+bΘ§«“x=70 ±Θ§y=50ΘΜx=80 ±Θ§y=40Θ°
Θ®1Θ©«σ“Μ¥ΈΚ· ΐy=kx+bΒΡ±μ¥ο ΫΘ§≤Δ»ΖΕ®Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®2Θ©»τΗΟ…Χ≥ΓΜώΒΟάϊ»σΈΣw‘ΣΘ§œζ έΒΞΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§…Χ≥ΓΩ…ΜώΒΟΉν¥σάϊ»σΘ§Ήν¥σάϊ»σ «Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2020Ρξ8‘¬ΗΏ” ΗΏΧζΫΪΆ®≥ΒΘ§ΗΏ” ÷Ν±±Ψ©ΒΡ¬Ζ≥Χ‘ΦΈΣ900kmΘ§ΦΉΓΔ““ΝΫ»Υ¥”ΗΏ” ≥ωΖΔΘ§Ζ÷±π≥ΥΉχΤϊ≥ΒA”κΗΏΧζB«ΑΆυ±±Ψ©Θ°“―÷ΣA≥ΒΒΡΤΫΨυΥΌΕ»±»B≥ΒΒΡΤΫΨυΥΌΕ»¬ΐ150km/hΘ§A≥ΒΒΡ–– Μ ±Φδ «B≥ΒΒΡ–– Μ ±ΦδΒΡ2.5±ΕΘ§ΝΫ≥ΒΒΡ–– Μ ±ΦδΖ÷±πΈΣΕύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷Ϋ…œ”–5Ηω±Ώ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫ–ΈΉι≥…ΒΡ÷ΫΤ§Θ°Ω…“‘”Οœ¬ΟφΒΡΖΫΖ®Α―ΥϋΦτΤ¥≥…“ΜΗω’ΐΖΫ–ΈΘ°
Θ®1Θ©Τ¥≥…ΒΡ’ΐΖΫ–ΈΒΡΟφΜΐ «Εύ…ΌΘ§±Ώ≥Λ «Εύ…ΌΘ°
Θ®2Θ©ΡψΡή‘Ύ3ΓΝ3ΒΡ’ΐΖΫ–ΈΖΫΗώΆΦ3÷–Θ§Ν§Ϋ”ΥΡΗωΒψΉι≥…ΟφΜΐΈΣ5ΒΡ’ΐΖΫ–Έ¬πΘΩ
Θ®3Θ©»γΆΦ4Θ§ΡψΡήΑ―’β °Ηω–Γ’ΐΖΫ–ΈΉι≥…ΒΡΆΦ–Έ÷ΫΘ§ΦτΩΣ≤ΔΤ¥≥…“ΜΗω¥σ’ΐΖΫ–Έ¬πΘΩ»τΡήΘ§«κΜ≠≥ω Ψ“βΆΦΘ§≤Δ–¥≥ω±Ώ≥ΛΈΣΕύ…ΌΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§ΨΊ–ΈABCD÷–Θ§ABΘΫ4cmΘ§BCΘΫ8cmΘ§ACΒΡ¥Ι÷±ΤΫΖ÷œΏEFΖ÷±πΫΜADΓΔBC”ΎΒψEΓΔFΘ§¥ΙΉψΈΣOΘ°

Θ®1Θ©»γΆΦ1Θ§Ν§Ϋ”AFΓΔCEΘ°«σ÷ΛΘΚΥΡ±Ώ–ΈAFCEΈΣΝβ–ΈΘ°
Θ®2Θ©»γΆΦ1Θ§«σAFΒΡ≥ΛΘ°
Θ®3Θ©»γΆΦ2Θ§Ε·ΒψPΓΔQΖ÷±π¥”AΓΔCΝΫΒψΆ§ ±≥ωΖΔΘ§―ΊΓςAFBΚΆΓςCDEΗς±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ήΘ°Φ¥ΒψPΉ‘AΓζFΓζBΓζAΆΘ÷ΙΘ§ΒψQΉ‘CΓζDΓζEΓζCΆΘ÷ΙΘ°‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΒψPΒΡΥΌΕ»ΈΣΟΩΟκ1cmΘ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ°
ΔΌΈ ‘Ύ‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§“‘AΓΔPΓΔCΓΔQΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ”–Ω…Ρή «ΨΊ–Έ¬πΘΩ»τ”–Ω…ΡήΘ§«κ«σ≥ω‘ΥΕ· ±ΦδtΚΆΒψQΒΡΥΌΕ»ΘΜ»τ≤ΜΩ…ΡήΘ§«κΥΒΟςάμ”…Θ°
ΔΎ»τΒψQΒΡΥΌΕ»ΈΣΟΩΟκ0.8cmΘ§Β±AΓΔPΓΔCΓΔQΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–Έ ±Θ§«σtΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ‘ΎΒΎ“Μœσœό«“Βψ
‘ΎΒΎ“Μœσœό«“Βψ![]() ΒΡΉίΉχ±ξΈΣ
ΒΡΉίΉχ±ξΈΣ![]() Θ°Β±
Θ°Β±![]() «―ϋ≥ΛΈΣ
«―ϋ≥ΛΈΣ![]() ΒΡΒ»―ϋ»ΐΫ«–Έ ±Θ§‘ρΒψ
ΒΡΒ»―ϋ»ΐΫ«–Έ ±Θ§‘ρΒψ![]() ΒΡΉχ±ξΈΣ_____Θ°
ΒΡΉχ±ξΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≥ωΉβ≥ΒΥΨΜζ–ΓάνΡ≥Χλ…œΈγ”Σ‘Υ ± «‘ΎΕΪΈςΉΏœρΒΡ¥σΫ÷…œΫχ––ΒΡΘ§»γΙϊΙφΕ®œρΕΪΈΣ’ΐΘ§œρΈςΈΣΗΚΘ§Υϊ’βΧλ…œΈγΥυΫ”ΝυΈΜ≥ΥΩΆΒΡ––≥Βάο≥ΧΘ®ΒΞΈΜΘΚ![]() Θ©»γœ¬ΘΚ
Θ©»γœ¬ΘΚ
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Έ ΘΚΘ®1Θ©ΫΪΉνΚσ“ΜΈΜ≥ΥΩΆΥΆΒΫΡΩΒΡΒΊ ±Θ§–Γάν‘Ύ ≤Ο¥ΈΜ÷ΟΘΩ
Θ®2Θ©»τΤϊ≥ΒΚΡ”ΆΝΩΈΣ![]() Θ®…ΐ/«ßΟΉΘ©Θ§’βΧλ…œΈγ–ΓάνΫ”ΥΆ≥ΥΩΆΘ§≥ωΉβ≥ΒΙ≤ΚΡ”ΆΕύ…Ό…ΐΘΩ
Θ®…ΐ/«ßΟΉΘ©Θ§’βΧλ…œΈγ–ΓάνΫ”ΥΆ≥ΥΩΆΘ§≥ωΉβ≥ΒΙ≤ΚΡ”ΆΕύ…Ό…ΐΘΩ
Θ®3Θ©»τ≥ωΉβ≥ΒΤπ≤ΫΦέΈΣ8‘ΣΘ§Τπ≤Ϋάο≥ΧΈΣ![]() Θ®Αϋά®
Θ®Αϋά®![]() Θ©Θ§≥§Ιΐ≤ΩΖ÷ΟΩ«ßΟΉ1.2‘ΣΘ§Έ –Γάν’βΧλ…œΈγΙ≤ΒΟ≥ΒΖ―Εύ…Ό‘ΣΘΩ
Θ©Θ§≥§Ιΐ≤ΩΖ÷ΟΩ«ßΟΉ1.2‘ΣΘ§Έ –Γάν’βΧλ…œΈγΙ≤ΒΟ≥ΒΖ―Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com