
����Ŀ����֪������ABCD�У�AB��4cm��BC��8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��

��1����ͼ1������AF��CE����֤���ı���AFCEΪ���Σ�
��2����ͼ1����AF�ij���
��3����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���P���ٶ�Ϊÿ��1cm�����˶�ʱ��Ϊt�룮
�������˶��Ĺ����У���A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��������п��ܣ�������˶�ʱ��t�͵�Q���ٶȣ��������ܣ���˵�����ɣ�
������Q���ٶ�Ϊÿ��0.8cm����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
���𰸡���1��֤������������2��AF��5cm����3�����п����Ǿ��Σ�P���˶���ʱ����8��Q���ٶ���0.5cm/s����t��![]() ��
��
��������
��1��֤��AEO�ա�CFO���Ƴ�OE=OF������ƽ���ı��κ����ε��ж��Ƴ����ɣ�
��2����AF=CF=a�����ݹ��ɶ����ó�����a�ķ��̣�������ɣ�
��3����ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��Σ����ʱ��t����������𰸣��ڷ�Ϊ���������P��AF�ϣ�P��BF�ϣ�P��AB�ϣ�����ƽ���ı��ε�����������ɣ�
��1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���AEO����CFO��
��AC�Ĵ�ֱƽ����EF��
��AO��OC��AC��EF��
����AEO����CFO��
��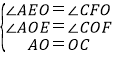 ��
��
���AEO�ա�CFO��AAS����
��OE��OF��
��OA��OC��
���ı���AECF��ƽ���ı��Σ�
��AC��EF��
��ƽ���ı���AECF�����Σ�
��2���⣺��AF��acm��
���ı���AECF�����Σ�
��AF��CF��acm��
��BC��8cm��
��BF����8��a��cm��
��Rt��ABF�У��ɹ��ɶ����ã�42+��8��a��2��a2��
a��5��
��AF��5cm��
��3���⣺�����˶������У���A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
P���˶���ʱ���ǣ���5+3����1��8��
Q���ٶ��ǣ�4��8��0.5��
��Q���ٶ���0.5cm/s��
�ڷ�Ϊ�����������һ��P��AF�ϣ�
��P���ٶ���1cm/s����Q���ٶ���0.8cm/s��
��Qֻ����CD�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
�ڶ�����P��BF��ʱ��Q��CD��DE�ϣ�ֻ�е�Q��DE��ʱ����A��P��C��Q�ĵ�Ϊ������ı��β��п�����ƽ���ı��Σ���ͼ��
��AQ��8����0.8t��4����CP��5+��t��5����
��8����0.8t��4����5+��t��5����
t��![]() ��
��
�����������P��AB��ʱ��Q��DE��CE�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
��t��![]() ��
��



 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ҫ�ڹ涨ʱ��������1400��ij��������ù�����һ���ٶȼӹ�5����ְ����ٶȼӹ���ȥ������10���깤�������ֳ����һ������Ͷ�����������������ʹ����Ч�������50%�����������ɼӹ�����
��1����ù���ǰ5��ÿ���������ٸ����������
��2����涨ʱ���Ƕ����죮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������AB��CD��ˮƽ����BCΪ60m����A����D��ĸ��Ǧ�Ϊ30�㣬���C��ĸ��Ǧ�Ϊ45�㣬������AB��CD�ĸ߶ȣ�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��y=ax2+bx�� ![]() ��a��0��������A��1��0����B����3��0����
��a��0��������A��1��0����B����3��0����
��1����������C1�Ľ���ʽ����д���䶥��C�����꣮
��2����ͼ1����������C1����ֱ��AC����ƽ�Ƶ�ij��ʱ�õ�������C2 �� ��ʱ��A��C�ֱ�ƽ�Ƶ���D��E�������F��������C1������x����Ϸ�������DEF����EFΪ�ĵ���ֱ�������Σ����F�����꣮
��3����ͼ2���ڣ�2���������£����M���߶�BC��һ���㣬EN��EM��ֱ��BF�ڵ�N����PΪ�߶�MN���е㣬����M�ӵ�B���C�˶�ʱ����tan��ENM��ֵ��α仯����˵�����ɣ��ڵ�M�����Cʱ��ֱ��д����P������·�߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC�ĵױ�BC��13cm��D����AB��һ�㣬��CD��12cm�� BD��5cm��
��1����֤����BDC��ֱ�������Σ�
��2������ABC���ܳ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
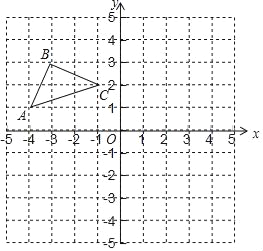
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��֪��ABC������������ֱ�ΪA����4��1����B����3��3����C����1��2����
��1��������ABC����x��ԳƵ���A1B1C1����A��B��C�ĶԳƵ�ֱ��ǵ�A1��B1��C1��ֱ��д����A1��B1��C1�����ꣻ
��2��������C����y��ĶԳƵ�C2������C1C2��CC2��C1C������CC1C2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������A��B������Ʒ��ÿ�ι���ͬһ����Ʒ�ĵ�����ͬ��������Ϣ���±���

����������Ϣ����������⣺
��1����A��B������Ʒ�ĵ��ۣ�
��2���������ι�����������Ʒ��12������A����Ʒ������������B����Ʒ������2��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC����D��AB��һ����DF��AC�ڵ�E��AE��EC��DE��EF��������˵���У��١�ADE����EFC���ڡ�ADE����ECF����FEC��180�����ۡ�B����BCF��180������S��ABC��S�ı���DBCF.��ȷ����(����)

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̿���������д��:�����ǰѶ���ʽ![]() ��
��![]() ������ȫƽ��ʽ�������һ������ʽ������ȫƽ��ʽ�����dz������±���:������һ���ʵ�����ʹʽ���г�����ȫƽ��ʽ���ټ�ȥ����ʹ����ʽ�ӵ�ֵ�������ַ��������䷽��.�䷽����һ����Ҫ�Ľ���������ѧ�������������Խ�һ�����Ʋ��ֽܷ�Ķ���ʽ�ֽ���ʽ�����ܽ��һЩ��Ǹ����йص����������ʽ���ֵ.��Сֵ��.
������ȫƽ��ʽ�������һ������ʽ������ȫƽ��ʽ�����dz������±���:������һ���ʵ�����ʹʽ���г�����ȫƽ��ʽ���ټ�ȥ����ʹ����ʽ�ӵ�ֵ�������ַ��������䷽��.�䷽����һ����Ҫ�Ľ���������ѧ�������������Խ�һ�����Ʋ��ֽܷ�Ķ���ʽ�ֽ���ʽ�����ܽ��һЩ��Ǹ����йص����������ʽ���ֵ.��Сֵ��.
����:�ֽ���ʽ
![]() �����������ʽ
�����������ʽ![]() ����Сֵ.
����Сֵ.![]() .��֪��
.��֪��![]() ʱ��
ʱ��![]() ����Сֵ����Сֵ��
����Сֵ����Сֵ��![]() �������Ķ��������䷽������������⣺
�������Ķ��������䷽������������⣺
��1���ֽ���ʽ:![]() _____
_____
��2����![]() Ϊ��ֵʱ������ʽ
Ϊ��ֵʱ������ʽ![]() ����Сֵ������������Сֵ.
����Сֵ������������Сֵ.
��3����![]() Ϊ��ֵʱ.����ʽ
Ϊ��ֵʱ.����ʽ![]() ����Сֵ����������Сֵ
����Сֵ����������Сֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com