Question

【题目】如图，两建筑物AB、CD的水平距离BC为60m，从A点测得D点的俯角α为30°，测得C点的俯角β为45°，求建筑物AB、CD的高度．（结果保留根号）

Answer 1

【答案】解：过点D作DE⊥AB于点E，则四边形BCDE是矩形，

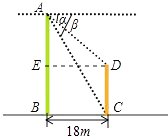
由题意得，∠ACB=β=60°，∠ADE=α=30°，BC=60m，

∴DE=BC=60m，CD=BE，

在Rt△ABC中，AB=BCtan∠ACB=60×tan60°=60 （m），

在Rt△ADE中，AE=DEtan∠ADE=60×tan30°=20 （m），

∴CD=BE=AB﹣AE=60 ﹣20 （m）．

答：建筑物AB、CD的高度分别为60 m、20 m．

【解析】过点D作DE⊥AB于点E，则四边形BCDE是矩形，由题意得，∠ACB=β=60°，∠ADE=α=30°，BC=60m，由矩形的性质得DE=BC=60m，CD=BE，解直角三角形得出AB,AE的长度，即可。
【考点精析】关于本题考查的关于仰角俯角问题，需要了解仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能得出正确答案．