
【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组![]()
现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
【答案】(1)代入消元法;加减消元法;基本思路都是消元;(2)![]() .
.
【解析】
(1)分析两种解法的具体方法,找出两种方法的共同点即可;
(2)将两种方法补充完整即可.
解:(1)解法一使用的具体方法是代入消元法,解法二使用的具体方法是加减消元法,以上两种方法的共同点是基本思路都是消元(或都设法消去了一个未知数,使二元问题转化为了一元问题);
故答案为:代入消元法,加减消元法,基本思路都是消元(或都设法消去了一个未知数,使二元问题转化为了一元问题);
(2)方法一:由①得:x=2y+5③,
把③代入②得:3(2y+5)﹣2y=3,
整理得:4y=﹣12,
解得:y=﹣3,
把y=﹣3代入③,得 x=﹣1,
则方程组的解为![]() ;
;
方法二:①﹣②,得﹣2x=2,
解得:x=﹣1,
把x=﹣1代入①,得﹣1﹣2y=5,
解得:y=﹣3,
则方程组的解为![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2. 
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( ) 
A.7.2 cm
B.5.4 cm
C.3.6 cm
D.0.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
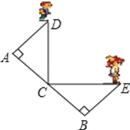
【题目】如图,C 是路段 AB 的中点,两人从 C 同时出发,以相同的速度分别沿两条直线行走,并同时到达 D,E 两地,DA⊥AB,EB⊥AB,D,E 与路段AB 的距离相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com