Question

【题目】如图，⊙ 的圆心 在反比例函数 的图像上，且与 轴、 轴相切于点 、 ，一次函数 的图像经过点 ，且与 轴交于点 ，与⊙ 的另一个交点为点 .

（1）求 的值及点 的坐标；
（2）求 长及 的大小；
（3）若将⊙ 沿 轴上下平移，使其与 轴及直线 均相切，求平移的方向及平移的距离.

Answer 1

【答案】
（1）解：如图1中，连接AC、AB．

∵⊙A与x轴、y轴相切于点B、C，

∴AC⊥OC，AB⊥OB，AC=AB，四边形ABOC是正方形，设A（m，m），

∵点A在y= 上，

∴m2=3，∵m＞0，

∴点A坐标（ ， ），

∴OC= ，

∴点C坐标（0， ），

∵一次函数y= x+b的图象经过点C，

∴b= ，

∴一次函数的解析式为y= ，

令y=0得x=-3，∴D（-3，0），b=

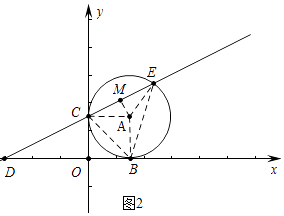
（2）解：如图2中，连接BC、BE，作AM⊥CE于M．

在Rt△DOC中，

∵tan∠CDO= ，

∴∠CDO=30°，

∵AC∥BD，

∴∠ECA=∠CDO=30°，∠CAM=60°，

∵AM⊥CE，

∴∠CAM=∠EAM=60°，

∴∠CAE=120°，

在Rt△AMC中，CM=ACcos30°= ，∴CE=2CM=3，∴∠CBE= ∠CAE=60°

（3）解：如图3中，

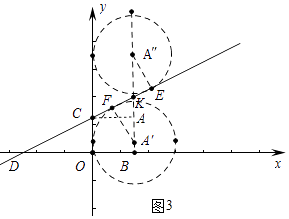
①当⊙A″与直线y= 相切于点E，AB与直线CD交于点K，

∵AB∥OC，

∴∠A″KE=∠DKB=∠DCO=60°，在Rt△A″EK中，A″E= ，A″K=A″E÷cos30°=2，在Rt△CKA中，AK=CAtan30°=1，

∴AA″=A″K+AK=1+2=3，

∴⊙A向上平移3的单位⊙A与y轴及直线y= 均相切．②同理可得⊙A向下平移1个单位⊙A与y轴及直线y= 均相切

【解析】（1）由⊙A与x轴、y轴相切于点B、C，得到四边形ABOC是正方形，由点A在反比例函数图像上，得到点A的坐标，求出OC的值，得到点C的坐标，由一次函数的图象经过点C，得到一次函数的解析式，得到点D的坐标，