
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
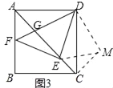
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

【答案】(1)①详见解析;②60°.(2)IH=![]() FH;(3)EG2=AG2+CE2.
FH;(3)EG2=AG2+CE2.
【解析】
(1)①由△DOE≌△BOF,推出EO=OF,∵OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可.
②先证明∠ABD=2∠ADB,推出∠ADB=30°,延长即可解决问题.
(2)IH=![]() FH.只要证明△IJF是等边三角形即可.
FH.只要证明△IJF是等边三角形即可.
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
(1)①证明:如图1中,
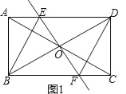
∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
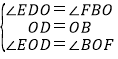 ,
,
∴△DOE≌△BOF,
∴EO=OF,∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,OB=OD,
∴EB=ED,
∴四边形EBFD是菱形.
②∵BE平分∠ABD,
∴∠ABE=∠EBD,
∵EB=ED,
∴∠EBD=∠EDB,
∴∠ABD=2∠ADB,
∵∠ABD+∠ADB=90°,
∴∠ADB=30°,∠ABD=60°,
∴∠ABE=∠EBO=∠OBF=30°,
∴∠EBF=60°.
(2)结论:IH=![]() FH.
FH.
理由:如图2中,延长BE到M,使得EM=EJ,连接MJ.

∵四边形EBFD是菱形,∠B=60°,
∴EB=BF=ED,DE∥BF,
∴∠JDH=∠FGH,
在△DHJ和△GHF中,
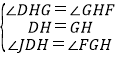 ,
,
∴△DHJ≌△GHF,
∴DJ=FG,JH=HF,
∴EJ=BG=EM=BI,
∴BE=IM=BF,
∵∠MEJ=∠B=60°,
∴△MEJ是等边三角形,
∴MJ=EM=NI,∠M=∠B=60°
在△BIF和△MJI中,
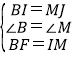 ,
,
∴△BIF≌△MJI,
∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,
∴IH⊥JF,
∵∠BFI+∠BIF=120°,
∴∠MIJ+∠BIF=120°,
∴∠JIF=60°,
∴△JIF是等边三角形,
在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,
∴∠FIH=30°,
∴IH=![]() FH.
FH.
(3)结论:EG2=AG2+CE2.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,
∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
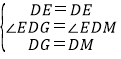 ,
,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边AD,CD上,

(1)若AB=6,AE=CF,点E为AD的中点,连接AE,BF.
①如图1,求证:BE=BF=3![]() ;
;
②如图2,连接AC,分别交AE,BF于M,M,连接DM,DN,求四边形BMDN的面积.
(2)如图3,过点D作DH⊥BE,垂足为H,连接CH,若∠DCH=22.5°,则![]() 的值为 (直接写出结果).
的值为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题: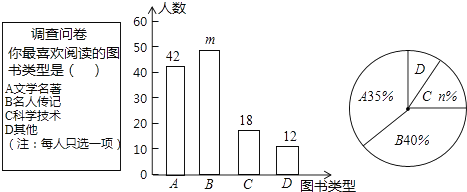
(1)本次调查共抽查了名学生,两幅统计图中的m= , n=.
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]()

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
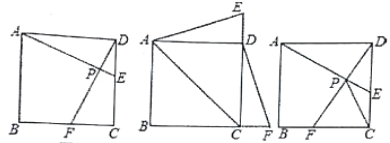
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 ![]() 、
、 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() 、
、 ![]() 、
、 ![]() ,先将
,先将 ![]() 沿一确定方向平移得到
沿一确定方向平移得到 ![]() ,点
,点 ![]() 的对应点
的对应点 ![]() 的坐标是
的坐标是 ![]() ,再将
,再将 ![]() 绕原点
绕原点 ![]() 顺时针旋转
顺时针旋转 ![]() 得到
得到 ![]() ,点
,点 ![]() 的对应点为点
的对应点为点 ![]() .
.
(1)画出 ![]() 和
和 ![]() ;
;
(2)求出在这两次变换过程中,点 ![]() 经过点
经过点 ![]() 到达
到达 ![]() 的路径总长;
的路径总长;
(3)求线段 ![]() 旋转到
旋转到 ![]() 所扫过的图形的面积.
所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙ ![]() 的圆心
的圆心 ![]() 在反比例函数
在反比例函数 ![]() 的图像上,且与
的图像上,且与 ![]() 轴、
轴、 ![]() 轴相切于点
轴相切于点 ![]() 、
、 ![]() ,一次函数
,一次函数 ![]() 的图像经过点
的图像经过点 ![]() ,且与
,且与 ![]() 轴交于点
轴交于点 ![]() ,与⊙
,与⊙ ![]() 的另一个交点为点
的另一个交点为点 ![]() .
.
(1)求 ![]() 的值及点
的值及点 ![]() 的坐标;
的坐标;
(2)求 ![]() 长及
长及 ![]() 的大小;
的大小;
(3)若将⊙ ![]() 沿
沿 ![]() 轴上下平移,使其与
轴上下平移,使其与 ![]() 轴及直线
轴及直线 ![]() 均相切,求平移的方向及平移的距离.
均相切,求平移的方向及平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com