
【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
【答案】(1)甲种纪念品购买了40件,乙种纪念品购买了60件;(2)共有两种方案,分别为方案一:购买甲种纪念品34件,乙种纪念品66件;方案二:购买甲种纪念品35件,乙种纪念品65件,其中方案一所需总费用最少,最少总费用是9360元.
【解析】
(1)设甲种纪念品购买了x件,乙种纪念品购买了(100﹣x)件,利用购买甲、乙两种纪念品一共花费了9600元列方程120x+80(100﹣x)=9600,然后解方程求出x,再计算(100﹣x)即可;
(2)设购买甲种纪念品m件,乙种奖品购买了(100﹣m)件,利用购买乙种纪念品的件数不超过甲种奖品件数的2倍,总花费不超过9400元列不等式组,然后解不等式组后确定x的整数值即可得到组委会的购买方案.
解:(1)设甲种纪念品购买了x件,乙种纪念品购买了(100﹣x)件,
根据题意得120x+80(100﹣x)=9600,
解得x=40,
则100﹣x=60,
答:甲种纪念品购买了40件,乙种纪念品购买了60件;
(2)设购买甲种纪念品m件,乙种奖品购买了(100﹣m)件,
根据题意,得 ![]() ,
,
解得 ![]() ≤m≤35,
≤m≤35,
∵m为整数,
∴m=34或m=35,
方案一:当m=34时,100﹣m=66,费用为:34×120+66×80=9360(元)
方案二:当m=35时,100﹣m=65,费用为:35×120+65×80=9400(元)
由于9400>9360,
所以方案一的费用低,费用为9360元.
答:共有两种方案,分别为方案一:购买甲种纪念品34件,乙种纪念品66件;方案二:购买甲种纪念品35件,乙种纪念品65件,其中方案一所需总费用最少,最少总费用是9360元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.
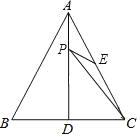
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
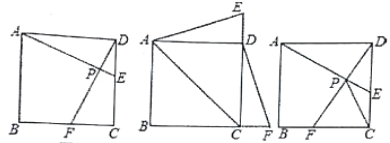
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙ ![]() 的圆心
的圆心 ![]() 在反比例函数
在反比例函数 ![]() 的图像上,且与
的图像上,且与 ![]() 轴、
轴、 ![]() 轴相切于点
轴相切于点 ![]() 、
、 ![]() ,一次函数
,一次函数 ![]() 的图像经过点
的图像经过点 ![]() ,且与
,且与 ![]() 轴交于点
轴交于点 ![]() ,与⊙
,与⊙ ![]() 的另一个交点为点
的另一个交点为点 ![]() .
.
(1)求 ![]() 的值及点
的值及点 ![]() 的坐标;
的坐标;
(2)求 ![]() 长及
长及 ![]() 的大小;
的大小;
(3)若将⊙ ![]() 沿
沿 ![]() 轴上下平移,使其与
轴上下平移,使其与 ![]() 轴及直线
轴及直线 ![]() 均相切,求平移的方向及平移的距离.
均相切,求平移的方向及平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

查看答案和解析>>
科目:初中数学 来源: 题型:
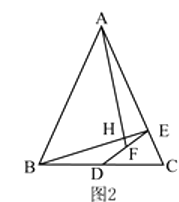
【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如何把多项式x2+8x+15因式分解?
(1)观察:上式能否可直接利用完全平方公式进行因式分解? 答: ;
(阅读与理解):由多项式乘法,我们知道(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左地使用,即可对形如x2+(a+b)x+ab的多项式进行因式分解,即:
x2+(a+b)x+ab=(x+a)(x+b)
此类多项式x2+(a+b)x+ab的特征是二次项系数为1,常数项为两数之积,一次项系数为这两数之和.
(2)猜想并填空: x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )
(3)上面多项式x2+8x+15的因式分解是否正确,我们需要验证.请写出验证过程.
(4)请运用上述方法将下列多项式进行因式分解:
① x2+8x+12 ② x2-x-12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com