【题目】如图，△ABC和△ADE中,AB=AD,AC=AE, ∠BAC＝∠DAE,BC交

DE于点O，∠BAD=ａ.

(1)求证：∠BOD=ａ.

(2)若AO平分∠DAC, 求证：AC=AD.

(3)若∠C=30°，OE交AC于F,且△AOF为等腰三角形，则ａ= .

参考答案：

【答案】（1）证明见解析；（2）证明见解析；（3）40°或20°

【解析】试题分析：（1）根据全等三角形的判定“SAS”证得△ABC≌△ADE，然后根据全等的性质，可得∠B=∠D，再根据三角形的内角和定理得证结论；

（2）过A作AM⊥BC于M，作AN⊥DE于N，由（1）知△ABC≌△ADE，根据全等三角形的面积相等，证得AM=AN，从而AO为∠DAC的平分线，根据ASA证得△ABO≌△AEO，可得AB=AE，然后得证；

（3）由题意可分为OA=OF和OA=AF两种情况讨论，即可求解.

试题解析：（1）在△ABC和△ADE中，

∵

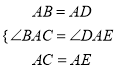
∴△ABC≌△ADE（SAS）∴∠B=∠D，∴∠BOD=∠BAD=α，

（2）过A作AM⊥BC于M，作AN⊥DE于N，

∵△ABC≌△ADE，∴S△ABC=S△ADE，∴，∵BC=DE，∴AM=AN，

∴AO平分∠BOE，∵AO平分∠DAC，∴∠DAO=∠CAO，∴∠BAO=∠EAO，

在△ABO和△AEO中，

∵

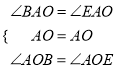
∴△ABO≌△AEO（ASA），

∴AB=AE，∵AB=AD，AC=AE，∴AC=AD，

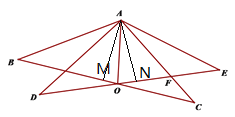
（3）当AO=AF时，a=40°，

当OA=OF时，a=20°，

故答案为：40°或20°.

关闭