
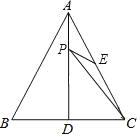
【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
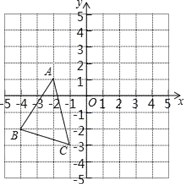
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_____秒时,△BCA与点P、N、B为顶点的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
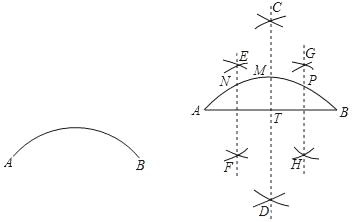
【题目】阅读下面材料:
在数学课上,老师请同学们思考如下问题:
请利用直尺和圆规四等分弧AB.
小亮的作法如下:
如图,
(1)连接AB;
(2)作AB的垂直平分线CD交弧AB于点M.交AB于点T;
(3)分别作线段AT,线段BT的垂直平分线EF,GH,交弧AB于N,P两点;
那么N,M,P三点把弧AB四等分.
老师问:“小亮的作法正确吗?”
请回备:小亮的作法_____(“正确”或“不正确”)理由是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )

A. 2B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2部甲型号手机和1部乙型号手机,共需要资金2800元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每部进价为多少元;
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台;若售出一部甲种型号手机,利润率为40%,乙型号手机的售价为1180元.为了获得最多的利润,应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.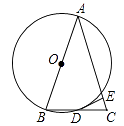
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 交x轴于A,交y轴于B,过B作
交x轴于A,交y轴于B,过B作![]() ,且
,且![]() ,点C在第四象限,点
,点C在第四象限,点![]() .
.
![]() 求点A,B,C的坐标;
求点A,B,C的坐标;
![]() 点M是直线AB上一动点,当
点M是直线AB上一动点,当![]() 最小时,求点M的坐标;
最小时,求点M的坐标;
![]() 点P、Q分别在直线AB和BC上,
点P、Q分别在直线AB和BC上,![]() 是以RQ为斜边的等腰直角三角形
是以RQ为斜边的等腰直角三角形![]() 直接写出点P的坐标.
直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com