
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2部甲型号手机和1部乙型号手机,共需要资金2800元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每部进价为多少元;
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台;若售出一部甲种型号手机,利润率为40%,乙型号手机的售价为1180元.为了获得最多的利润,应如何进货?
【答案】(1)甲型号手机每部进价为1000元,乙型号手机每部进价为800元;(2)进货方案为甲种型号和乙种型号手机各进10部.
【解析】
(1)设甲种型号手机每部进价为x元,乙种型号手机每部进价为y元,根据题意建立方程组求解就可以求出答案;
(2)设购进甲种型号手机a部,则购进乙种型号手机(20-a)部,根据“用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台”建立不等式组,求出其解就可以得出结论.
解:(1)设甲种型号手机每部进价为![]() 元,乙种型号手机每部进价为
元,乙种型号手机每部进价为![]() 元
元
![]() ,
,
解得![]() ,
,
答:甲型号手机每部进价为1000元,乙型号手机每部进价为800元;
(2)设购进甲种型号手机![]() 部,则购进乙种型号手机
部,则购进乙种型号手机![]() 部,
部,
![]() ,
,
解得![]() ,
,
∵![]() 为整数,可以取7、8、9、10
为整数,可以取7、8、9、10
∴共有四种方案,
甲种型号手机每部利润为![]() ,
,
设所获利润为![]() 元,由题意得:
元,由题意得:![]()
∵![]() ,∴
,∴![]() 随
随![]() 的增大而增大
的增大而增大
当![]() 时,会获得最大利润.
时,会获得最大利润.
![]()
答:进货方案为甲种型号和乙种型号手机各进10部


科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,坚持绿色发展,建设美丽家园,青年大学生小王准备在家乡边疆种植两种树木.经研究发现,A种树木种植费用y(元)与 种植面积 x(m2)的函数表达式如图所示,B种树木的种植费用为400元/ m2.
(1)求y与x的函数表达式;
(2)A种树木和 B 种树木种植面积共 1500 m,若A种树木种植面积不超过B种树木种 植面积的2倍,且 A 种树木种植面积不少于 400 m,应该如何分配A种树木和B种树木的种植面积才能使得总费用最少?最少费用是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
A.4:25
B.4:9
C.9:25
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.
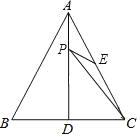
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
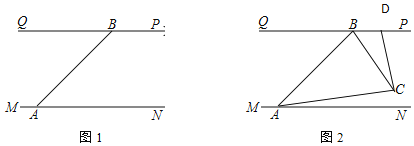
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com