
【题目】为践行“绿水青山就是金山银山”的理念,坚持绿色发展,建设美丽家园,青年大学生小王准备在家乡边疆种植两种树木.经研究发现,A种树木种植费用y(元)与 种植面积 x(m2)的函数表达式如图所示,B种树木的种植费用为400元/ m2.
(1)求y与x的函数表达式;
(2)A种树木和 B 种树木种植面积共 1500 m,若A种树木种植面积不超过B种树木种 植面积的2倍,且 A 种树木种植面积不少于 400 m,应该如何分配A种树木和B种树木的种植面积才能使得总费用最少?最少费用是多少?

【答案】(1)y=![]() ;(2) 应该分配A、B两种花卉的种植面积分别是800m2 和700m2,才能使种植总费用最少,最少总费用为530000元.
;(2) 应该分配A、B两种花卉的种植面积分别是800m2 和700m2,才能使种植总费用最少,最少总费用为530000元.
【解析】
(1)由图可知y与x的函数关系式是分段函数,待定系数法求解析式即可.
(2)设A种花卉种植为 a m2,则B种花卉种植(1500-a)m2,根据实际意义可以确定a的范围,结合种植费用y(元)与种植面积x(m2)之间的函数关系可以分类讨论最少费用为多少.
解:当0≤x≤500时,设y=kx,即500k=25000,解得k=500,即可y=500x;
当x≥500时,设y=kx+b,根据题意得,![]() ,解得
,解得
![]() ,故y=300x+100000,
,故y=300x+100000,
故y与x的函数表达式为:y=![]() ;
;
(2)设A种花卉种植为 a m2,则B种花卉种植(1500-a)m2.
∴![]() ,
,
∴400≤a≤1000
当400≤a≤500时,W1=500a+400(1500-a)=100a+600000.
当a=400 时.Wmin=640000 元
当500≤a≤1000时,W2=300a+100000+400(1500-a)=700000-100a.
当a=1000时,Wmin=600000 元
∵600000<640000,
∴当a=800时,总费用最少,最少总费用,600000元.
此时B种花卉种植面积为1500-800=700m2.
答:应该分配A、B两种花卉的种植面积分别是800m2 和700m2,才能使种植总费用最少,最少总费用为600000元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA,OB的长和经过点A,B,C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
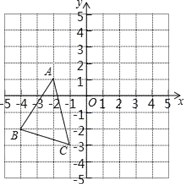
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线 ![]() 的顶点为
的顶点为 ![]() ,与
,与 ![]() 轴的一个交点
轴的一个交点 ![]() 在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:①
在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:① ![]() <0 ;②
<0 ;② ![]() <0;③
<0;③ ![]() =2;④方程
=2;④方程 ![]() 有两个相等的实数根,其中正确结论的个数为个.
有两个相等的实数根,其中正确结论的个数为个.
查看答案和解析>>
科目:初中数学 来源: 题型:
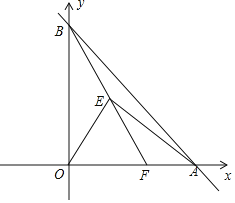
【题目】如图,在直角坐标系中,直线![]() 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点![]() ,点E在第一象限,
,点E在第一象限,![]() 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE
![]() 求点E的坐标;
求点E的坐标;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,求
的面积分为3:1时,求![]() 的面积;
的面积;
![]() 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当![]() 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则![]() ______
______![]() 直接写出b的值
直接写出b的值![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B( ![]() ,y1),C(
,y1),C( ![]() ,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是 .
,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2部甲型号手机和1部乙型号手机,共需要资金2800元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每部进价为多少元;
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台;若售出一部甲种型号手机,利润率为40%,乙型号手机的售价为1180元.为了获得最多的利润,应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com