Question

【题目】已知：Rt△ABC的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB与x轴重合（其中OA＜OB），直角顶点C落在y轴正半轴上（如图1）．

（1）求线段OA,OB的长和经过点A，B，C的抛物线的关系式．
（2）如图2，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点（其中m＞0，n＞0），连接DP交BC于点E．
①当△BDE是等腰三角形时，直接写出此时点E的坐标．
②又连接CD、CP（如图3），△CDP是否有最大面积？若有，求出△CDP的最大面积和此时点P的坐标；若没有，请说明理由．

Answer 1

【答案】
（1）解：设OA的长为x，则OB=5﹣x；

∵OC=2，AB=5，∠BOC=∠AOC=90°，∠OAC=∠OCB；

∴△AOC∽△COB，∴OC2=OAOB

∴22=x（5﹣x）

解得：x1=1，x2=4，

∵OA＜OB，∴OA=1，OB=4；

∴点A、B、C的坐标分别是：A（﹣1，0），B（4，0），C（0，2）；

方法一：设经过点A、B、C的抛物线的关系式为：y=ax2+bx+2，

将A、B、C三点的坐标代入得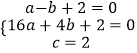

解得：a= ，b= ，c=2

所以这个二次函数的表达式为：

方法二：设过点A、B、C的抛物线的关系式为：y=a（x+1）（x﹣4）

将C点的坐标代入得：a=

所以这个二次函数的表达式为：

（2）解：①当△BDE是等腰三角形时，点E的坐标分别是： ， ， ．

②如图1，连接OP，

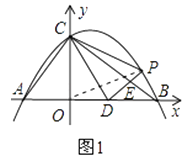
S△CDP=S四边形CODP﹣S△COD=S△COP+S△ODP﹣S△COD

= =m+n﹣2

= =

∴当m= 时，△CDP的面积最大．此时P点的坐标为（ ， ），

S△CDP的最大值是 ．

另解：如图2、图3，过点P作PF⊥x轴于点F，则

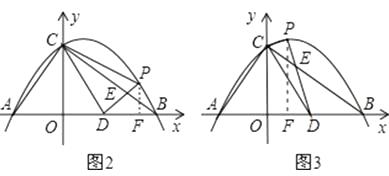
S△CDP=S梯形COFP﹣S△COD﹣S△DFP

= =m+n﹣2

= =

∴当m= 时，△CDP的面积最大．此时P点的坐标为（ ， ），

S△CDP的最大值是

【解析】（1）利用相似三角形的性质对应边成比例可列出比例式，构建方程；求出A、B、C坐标代入解析式即可 ；（2）△BDE是等腰三角形可分为三类：BD=BE或DB=DE或EB=ED；（3）最值问题的基本解决办法是函数思想，用m的代数式表示面积，通过P向x轴作垂线，构造梯形，作差法表示三角形面积，构建函数，利用配方法求出最值.