
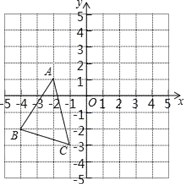
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
【答案】(1)(3,5),(1,2);(2)见解析;(3)![]() .
.
【解析】
(1)由点C(﹣1,﹣3)平移到C′(4,1)可知,图形的平移规律是:先向右平移5个单位,再向上平移4个单位,根据此规律即可求出A′、B′的坐标;
(2)描出A′、B′、C′三点的坐标,再依次连接即可;
(3)如图2,S△A'B'C'= S矩形C'EDF-S△A'C'F-S△A'B'D-S△B'C'E,再代入数据进行计算即可.
解:(1)由点C(﹣1,﹣3)平移到C′(4,1)可知,图形的平移规律是:先向右平移5个单位,再向上平移4个单位,所以A′、B′的坐标分别是(﹣2+5,1+4)、(﹣4+5,﹣2+4),即A′(3,5)、B′(1,2);
故答案为(3,5),(1,2);
(2)如图1,△A′B′C′即为所求.

(3)如图2,S△A'B'C'= S矩形C'EDF-S△A'C'F-S△A'B'D-S△B'C'E
=![]()
=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.

③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有火车车皮和货车可供租用,货主准备租用火车车皮和货车运输一批物资,已知以往用这种火车车皮和货车运货情况如下表:
第一次 | 第二次 | |
火车车皮(节) | 6 | 8 |
货车(辆) | 15 | 10 |
累计运货(吨) | 360 | 440 |
(1)每节火车车皮和每辆货车平均各装物资多少吨?
(2)若货主需要租用该公司的火车车皮7节,货车10辆,刚好运完这批货物,如按每吨付运费60元,则货主应付运费总额为多少元?
(3)若货主共有300吨货,计划租用该公司的火车车皮或货车正好(每节车皮和每辆货车都满载)把这批货运完,该公司共有哪几种运货方案?写出所有的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,坚持绿色发展,建设美丽家园,青年大学生小王准备在家乡边疆种植两种树木.经研究发现,A种树木种植费用y(元)与 种植面积 x(m2)的函数表达式如图所示,B种树木的种植费用为400元/ m2.
(1)求y与x的函数表达式;
(2)A种树木和 B 种树木种植面积共 1500 m,若A种树木种植面积不超过B种树木种 植面积的2倍,且 A 种树木种植面积不少于 400 m,应该如何分配A种树木和B种树木的种植面积才能使得总费用最少?最少费用是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
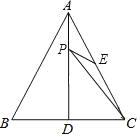
【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com