
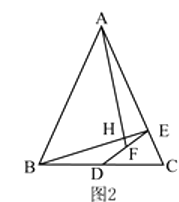
【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
【答案】
(1)解:如图1,连接AD,
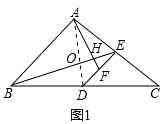
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC= ![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,∴ ![]() ,即ADCE=BDDE.
,即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD= ![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═ ![]() BC2DF=BCDF,
BC2DF=BCDF,
∴ ![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴ ![]() ,在Rt△ADB中,
,在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°- ![]() ∠BAC,BD=
∠BAC,BD= ![]() BC,
BC,
∴tan∠ABD=tan(90°- ![]() ∠BAC)=
∠BAC)= ![]() ,
,
∴ ![]() =
= ![]() tan(90°-
tan(90°- ![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() ×90°)=
×90°)= ![]() ;∴AF⊥BE,
;∴AF⊥BE, ![]() =
= ![]()
(2)解:如图2,
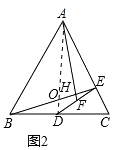
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() α);∴AF⊥BE, =
α);∴AF⊥BE, = ![]() tan(90°-
tan(90°- ![]() α)
α)
【解析】(1)由AB=AC,点D是BC的中点,根据三线合一,得到AD⊥BC,由DE⊥AC,根据同角的余角相等,得到∠ADE=∠C;得到△ADB∽△DEC,得到比例,即ADCE=BDDE;由已知得到ADCE=BCDF,又∠ADE=∠C,得到△AFD∽△BEC,得到比例,在Rt△ADB中,根据三角函数定义,得到∠DAF=∠CBE,由三角形内角和定理求出∠AHO=90°,即∠AHB=90°,根据以上结论可得![]()
【考点精析】掌握相似三角形的判定与性质和锐角三角函数的定义是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 交x轴于A,交y轴于B,过B作
交x轴于A,交y轴于B,过B作![]() ,且
,且![]() ,点C在第四象限,点
,点C在第四象限,点![]() .
.
![]() 求点A,B,C的坐标;
求点A,B,C的坐标;
![]() 点M是直线AB上一动点,当
点M是直线AB上一动点,当![]() 最小时,求点M的坐标;
最小时,求点M的坐标;
![]() 点P、Q分别在直线AB和BC上,
点P、Q分别在直线AB和BC上,![]() 是以RQ为斜边的等腰直角三角形
是以RQ为斜边的等腰直角三角形![]() 直接写出点P的坐标.
直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ![]() ,∠DPA=45°.
,∠DPA=45°.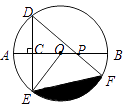
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组![]()
现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com