
【题目】如图,在等边 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() ,
, ![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() 的面积与
的面积与 ![]() 的面积之比等于( )
的面积之比等于( )
A.1∶3
B.2∶3
C.![]() ∶2
∶2
D.![]() ∶3
∶3
【答案】A
【解析】∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠C+∠EDC=90°,∠FDE+∠EDC=90°,
∴∠C=∠FDE,
同理可得:∠B=∠DFE,∠A=DEF,
∴△DEF∽△CAB,
∴△DEF与△ABC的面积之比= ![]() ,
,
又∵△ABC为正三角形,
∴∠B=∠C=∠A=60°
∴△EFD是等边三角形,
∴EF=DE=DF,
又∵DE⊥AC,EF⊥AB,FD⊥BC,
∴△AEF≌△CDE≌△BFD,
∴BF=AE=CD,AF=BD=EC,
在Rt△DEC中,
DE=DC×sin∠C= ![]() DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC= ![]() DC,
DC,
又∵DC+BD=BC=AC= ![]() DC,
DC,
∴  ,
,
∴△DEF与△ABC的面积之比等于: ![]()
所以答案是:A.
【考点精析】掌握相似三角形的判定与性质和解直角三角形是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
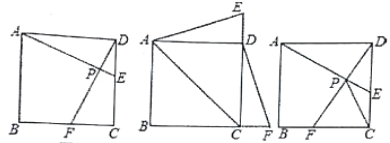
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

查看答案和解析>>
科目:初中数学 来源: 题型:
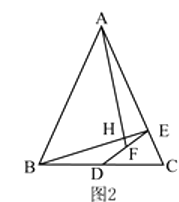
【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, ![]() 与
与 ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() 与
与 ![]() 重合,
重合, ![]() ,
, ![]() .固定
.固定 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 顺时针旋转,当
顺时针旋转,当 ![]() 边与
边与 ![]() 边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设
边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设 ![]() (或它们的延长线)分别交
(或它们的延长线)分别交 ![]() (或它们的延长线)于点
(或它们的延长线)于点 ![]() ,如图2.
,如图2.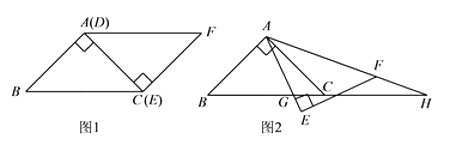
(1)证明: ![]() ;
;
(2)当 ![]() 为何值时,
为何值时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如何把多项式x2+8x+15因式分解?
(1)观察:上式能否可直接利用完全平方公式进行因式分解? 答: ;
(阅读与理解):由多项式乘法,我们知道(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左地使用,即可对形如x2+(a+b)x+ab的多项式进行因式分解,即:
x2+(a+b)x+ab=(x+a)(x+b)
此类多项式x2+(a+b)x+ab的特征是二次项系数为1,常数项为两数之积,一次项系数为这两数之和.
(2)猜想并填空: x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )
(3)上面多项式x2+8x+15的因式分解是否正确,我们需要验证.请写出验证过程.
(4)请运用上述方法将下列多项式进行因式分解:
① x2+8x+12 ② x2-x-12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com