
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ![]() ,∠DPA=45°.
,∠DPA=45°.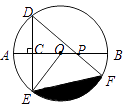
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
【答案】
(1)解:∵直径AB⊥DE,∴CE= ![]() DE=
DE= ![]() .
.
∵DE平分AO,
∴CO= ![]() AO=
AO= ![]() OE.又∵∠OCE=90°,
OE.又∵∠OCE=90°,
∴sin∠CEO= ![]() =
= ![]() ,
,
∴∠CEO=30°.在Rt△COE中,OE= ![]() =
= ![]() .
.
∴⊙O的半径为2
(2)解:连接OF.
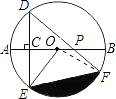
在Rt△DCP中,
∵∠DPC=45°,
∴∠D=90°﹣45°=45°.
∴∠EOF=2∠D=90°.
∴S扇形OEF= ![]() .
.
∵∠EOF=2∠D=90°,OE=OF=2,
∴SRt△OEF= ![]() ×OE×OF=2.
×OE×OF=2.
∴S阴影=S扇形OEF﹣SRt△OEF= ![]() .
.
【解析】(1)根据垂径定理求出CE的值,根据特殊角的三角函数值,求出⊙O的半径;(2)根据圆周角定理,求出∠EOF=2∠D的值,根据扇形的面积公式求出S扇形OEF的值,由△OEF的面积,得到S阴影=S扇形OEF﹣SRt△OEF的值.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.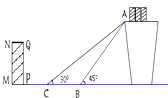
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物 ![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
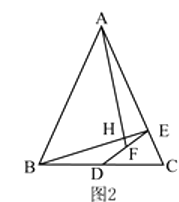
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, ![]() 与
与 ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() 与
与 ![]() 重合,
重合, ![]() ,
, ![]() .固定
.固定 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 顺时针旋转,当
顺时针旋转,当 ![]() 边与
边与 ![]() 边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设
边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设 ![]() (或它们的延长线)分别交
(或它们的延长线)分别交 ![]() (或它们的延长线)于点
(或它们的延长线)于点 ![]() ,如图2.
,如图2.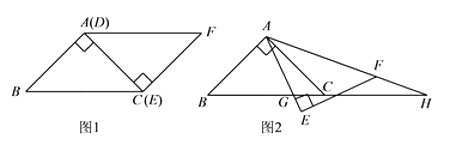
(1)证明: ![]() ;
;
(2)当 ![]() 为何值时,
为何值时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )

A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com